Abstrak
Dalam studi ini, dua model rangka dikembangkan untuk penyertaan serat baja: model rangka sudut putar yang disederhanakan dan model rangka ruang. Model-model ini menggabungkan kontribusi serat melalui pendekatan rasional, menghitung sudut penyangga kompresi menggunakan analogi rangka ruang dan menggunakan model keterlibatan variabel untuk menentukan kontribusi komponen serat terhadap kekuatan tarik web. Model-model tersebut memperhitungkan rotasi retak pasca-leleh dan memprediksi kekuatan torsi balok beton bertulang serat baja (SFRC). Selain itu, perilaku torsi balok SFRC dengan dan tanpa tulangan melintang konvensional diperiksa secara kritis melalui pengujian enam balok persegi panjang skala besar dengan dosis serat yang bervariasi (0, 30, dan 60 kg/m 3 ) dan konfigurasi tulangan melintang yang berbeda (tanpa tulangan melingkar, kode minimum 0,5, dan kode minimum 1,0). Studi ini menyoroti perbedaan yang signifikan dalam pola retak dan mekanisme kegagalan antara beton bertulang dan balok beton bertulang serat baja (R-SFRC). Balok R-SFRC tanpa tulangan melingkar konvensional menunjukkan daktilitas yang berkurang, sementara balok dengan setidaknya 50% tulangan melingkar minimum mempertahankan daktilitas yang sama dengan spesimen kontrol. Temuan tersebut merekomendasikan untuk mempertahankan setidaknya 50% tulangan melingkar torsional minimum dengan jarak sengkang tidak melebihi 75% dari kedalaman efektif penampang. Terakhir, model yang diusulkan diuji terhadap 63 spesimen yang dilaporkan dalam literatur (termasuk pengujian yang dilakukan dalam studi ini), yang menunjukkan korelasi yang kuat dengan data uji.
1. PENDAHULUAN
Struktur rangka penahan momen biasa, yang terdiri dari balok horizontal yang terhubung ke kolom vertikal, merupakan bentuk konstruksi yang umum. Rangka ini harus kuat, mampu menahan deformasi plastis yang besar selama peristiwa kelebihan beban, sekaligus mempertahankan kapasitas ketahanan beban. Torsi merupakan salah satu dari empat gaya internal utama dalam struktur, gaya tekuk, geser, dan gaya aksial merupakan gaya lainnya. Seiring dengan berkembangnya struktur modern dengan desain arsitektur yang cerdik, torsi pada elemen struktural menjadi lebih umum dan, dengan demikian, perilaku torsional anggota struktural beton bertulang (RC) merupakan bidang penelitian yang penting. 1
Selama lebih dari setengah abad, beton bertulang serat baja (SFRC) telah dipelajari secara ekstensif. Serat baja dapat mendistribusikan tegangan tarik di seluruh retakan pada matriks beton dan memungkinkan anggota struktural SFRC berperilaku daktail. SFRC meningkatkan kekuatan tarik sisa dan sifat mekanis beton lainnya, seperti penyerapan energi, kekuatan lelah, dan ketahanan terhadap beban impak. 2 – 5 Penelitian menunjukkan bahwa serat baja pada balok SFRC meningkatkan karakteristik deformasi dengan mengurangi kelengkungan, 6 , 7 berkontribusi pada kekuatan geser dengan mengganti sebagian sengkang konvensional, 8 – 11 meningkatkan kapasitas momen 12 – 15 dan secara signifikan meningkatkan kinerja lelah. 16 , 17
Penelitian substansial di seluruh dunia mengenai perilaku SFRC telah memberikan keyakinan untuk menggunakan serat baja guna menggantikan atau melengkapi tulangan utama dalam struktur RC. Berdasarkan data penelitian yang diperoleh selama lima dekade, kode dan standar desain utama 18 – 21 telah mengembangkan pedoman desain untuk elemen struktural SFRC. Sementara model desain ini memberikan estimasi yang baik untuk kapasitas geser dan lentur anggota SFRC, model tersebut belum mempertimbangkan kontribusi serat terhadap kekuatan torsional.
Namun, dengan kekuatan tarik sisa dan kapasitas rotasi yang lebih tinggi, diharapkan bahwa komponen beton bertulang serat baja (R-SFRC) akan menunjukkan kinerja torsi yang lebih baik. Beberapa penelitian eksperimental dan teori tentang perilaku torsi komponen R-SFRC, yang berupaya menangkap kontribusi serat baja, telah dilaporkan. 22 – 24 , 21 , 25 – 30
Uji coba awal yang dilakukan oleh Mansur dan Paramasivam 31 dan Narayanan dan Kareem-Palanjian 32 melaporkan peningkatan kapasitas momen torsional masing-masing sebesar 27% dan 25%, dengan penambahan serat baja. Baru-baru ini, Ju et al. 25 menunjukkan peningkatan kekuatan torsional balok R-SFRC sebesar 53% dan 81% dengan volume serat masing-masing sebesar 1,5% dan 2%, yang menunjukkan ketergantungan pada volume serat dan jenis serat.
Berbagai upaya telah dilakukan untuk mengembangkan model-model rasional guna memprediksi perilaku torsional anggota R-SFRC. Misalnya, Mansur et al. 28 menggabungkan model kekuatan tarik residual SFRC dari Lim et al. 27 ke dalam model rangka-lunak (STM) Hsu 33 untuk torsi anggota RC. Model torsi Mansur menunjukkan korelasi yang baik dengan data eksperimen untuk zona pascaretak; namun, model tersebut meremehkan kekakuan awal. Sekali lagi, dengan menggunakan STM, Rao dan Seshu 29 mengusulkan model torsional untuk menghitung kekakuan torsional awal secara lebih akurat. Baru-baru ini, variasi pada model rangka ruang (sTM) telah dikembangkan oleh Amin dan Bentz, 22 Facconi et al. 34 dan Oettel 35 untuk memprediksi kekuatan balok SFRC dalam torsi.
Karayannis 36 menguji 10 balok dalam torsi murni dengan fraksi volume serat yang bervariasi (1% dan 3%) dan geometri yang berbeda. Mereka juga mengusulkan model analitis untuk memprediksi kekuatan. Amin dan Bentz 22 menguji dua balok dalam torsi murni dan memeriksa 21 balok lebih lanjut yang dilaporkan dalam literatur. Mereka mengusulkan model prediksi kekuatan dengan kekuatan tarik SFRC yang ditentukan menggunakan model pengikatan variabel (VEM) dari Voo dan Foster. 37 Model ini dibahas di bawah ini. Terakhir, Facconi et al. 30 menguji 18 spesimen skala besar dalam torsi murni dengan dan tanpa tulangan melingkar konvensional dan berbagai dosis serat. Seperti halnya peneliti sebelumnya, mereka menemukan bahwa menambahkan serat baja meningkatkan kekakuan balok, mengurangi jarak retak dan lebar retak, dan meningkatkan kapasitasnya di bawah beban torsi. Berdasarkan hal ini dan perbandingan dengan penelitian lain, mereka mengusulkan model analitis. 34
Studi ini melaporkan pengujian enam balok penampang persegi panjang skala besar R-SFRC dalam torsi murni, dengan beberapa dosis serat yang berbeda (nominal nol, 30, dan 60 kg/m 3 ) dan berbagai konfigurasi tulangan melintang (tanpa tulangan melingkar, minimum 0,5, dan minimum 1,0). Model dikembangkan berdasarkan (1) model rangka batang putar Hsu 33 yang disederhanakan (sRA-STM) dan (2) model rangka batang ruang yang disederhanakan (sSp-TM) yang cocok untuk menetapkan perilaku torsi R-SFRC, dengan tepat menangkap kontribusi serat baja, serta tulangan batang longitudinal dan melintang. Model dinilai berdasarkan 63 set data eksperimen yang dikumpulkan dari literatur (termasuk pengujian yang dilakukan dalam studi ini).
2 MODEL DESAIN UNTUK BALOK R-SFRC DALAM TORSI MURNI
2.1 Model rangka ruang
Dari sekian banyak ekspresi empiris dan teoritis yang diajukan, sTM adalah pendekatan yang paling sederhana dan paling rasional. 38 Teori analogi rangka batang dikembangkan oleh Ritter 39 dan Mörsch. 40 Berdasarkan karya mereka, Rausch 41 mengembangkan persamaan analogi rangka batang pertama untuk torsi. Model yang ditunjukkan pada Gambar 1 mempertimbangkan batang memanjang, tulangan melintang (lingkaran) dan penopang beton diagonal (beton di antara retakan). Lebih jauh, dengan memanfaatkan teori tabung Bredt, 42 Rausch 41 menghubungkan momen torsi T ke aliran geser q dengan:
![]()
di mana A o adalah area yang tercakup dalam garis tengah lintasan aliran geser (ditambah area lubang apa pun). Ini adalah area yang sama dengan A 0 = ( x – t d ) × ( y – t d ) pada Gambar 1 , di mana t d adalah ketebalan tabung ekivalen, dan x dan y adalah dimensi pendek dan panjang penampang balok, masing-masing. Rausch 41 mengasumsikan sudut penyangga menjadi 45° dan lintasan aliran geser sejajar dengan garis tengah lingkaran tertutup.
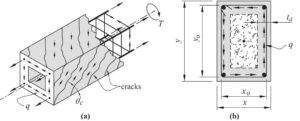
Collins dan Michell 43 mencatat bahwa pada balok beton padat yang mengalami torsi, penutup beton retak sebelum beban akhir tercapai. Oleh karena itu, mereka mengadopsi area yang dibatasi oleh garis tengah tulangan melingkar sebagai luas penampang efektif A oh = x o y o , di mana x o dan y o masing-masing adalah jarak yang lebih kecil dan lebih besar antara garis tengah tulangan melingkar (Gambar 1 ).
Akan tetapi, dalam teori tabung, penampang efektif berdinding tipis dengan ketebalan tabung, t d , dengan aliran geser konstan, q , diasumsikan menghasilkan momen torsional T yang sama dengan penampang balok persegi panjang. Ketebalan tabung, t d , merupakan fungsi geometri penampang, kekuatan beton, dan volume baja longitudinal dan transversal. Para peneliti telah menyarankan berbagai persamaan untuk memperkirakan t d . 44 , 45 Collins dan Mitchell 44 mendefinisikan t d sebagai berikut:
![]()
di mana A c adalah luas penampang bruto beton dan u c adalah keliling luar penampang bruto beton; yaitu, u c = 2( x + y ) pada Gambar 1. Dalam beberapa standar desain 18 , 19 , 46 luas A o diperkirakan sebesar 0,85 A oh , di mana A oh adalah yang didefinisikan oleh Collins dan Mitchell, 43 yang dibahas di atas.
Sejak pengembangan konseptual awal oleh Rausch, 41 pendekatan rangka untuk balok RC dalam torsi telah mengalami beberapa tahap perbaikan karena pemahaman yang lebih baik tentang perilaku torsi dan geser anggota RC telah berkembang. 38 , 47 – 49 Dalam pendekatan medan tegangan tekan, 49 juga disebut sebagai teori medan kompresi (CFT), diasumsikan bahwa beton yang retak tidak dapat membawa tegangan apa pun. Sambil menahan geser, penopang diagonal ini membawa tegangan tekan utama dalam kesetimbangan dengan gaya tarik pada gaya baja longitudinal dan melingkar (tarik). Mitchell dan Collins 49 juga mengusulkan bahwa regangan tekan utama adalah maksimum di permukaan dan bervariasi secara linear hingga nol pada kedalaman t d (Gambar 1 ) dan mengembangkan persamaan untuk menghitung sudut penopang, θ c dengan mengacu pada sumbu longitudinal ( l -). Jika penghancuran web tidak terjadi terlebih dahulu, CFT dapat memprediksi θ c berdasarkan luas dan kekuatan luluh tulangan longitudinal dan transversal (lingkaran) (Gambar 1 ).
Berdasarkan karya Mansur dkk., 28 Amin dan Bentz, 22 Facconi dkk., 34 dan Oettel 35 dalam pengembangan model untuk anggota R-SFRC, tegangan yang dipikul oleh serat dipertimbangkan sebagai tambahan terhadap tegangan yang dipikul oleh rangka dan baja longitudinal. Dengan mempertimbangkan model rangka, untuk menyeimbangkan kompresi diagonal pada penyangga, kapasitas torsional yang ditentukan secara terpisah dari tegangan pada masing-masing sumbu longitudinal ( l -) dan transversal ( t -) adalah:
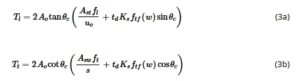
di mana T l dan T t adalah kekuatan torsional (momen) yang dibatasi oleh gaya tarik yang dipertahankan oleh tulangan longitudinal dan serat dan simpai dan serat, masing-masing, A st adalah total luas tulangan tarik longitudinal, A sw adalah luas satu kaki baja simpai, u o adalah keliling garis tengah lintasan aliran geser, s adalah jarak tulangan transversal atau simpai, fl l dan f t adalah tegangan pada tulangan longitudinal dan simpai, masing-masing, t d adalah tebal dinding tabung ekivalen, dan K s f tf ( w ) adalah tegangan efektif yang dibawa oleh serat untuk bukaan retak sebesar w . Dalam pengembangan Persamaan (3), diketahui bahwa bukaan retak torsional tegak lurus terhadap sudut retak θ c . Hal ini berbeda dengan aplikasi Amin dan Bentz, 22 Facconi et al., 34 dan Oettel, 35 di mana kontribusi serat terhadap kekuatan torsional dalam arah l dan t diasumsikan sama dengan kontribusi tarik pascaretak serat yang ditentukan secara uniaxial. Dalam kasus Oettel, hal ini dapat disesuaikan dengan bias dalam penyelarasan serat.
2.2 Sudut penyangga
Setelah retakan terbentuk, kondisi tegangan dan regangan pada dinding membran berubah. Tegangan tekan ditahan oleh penopang beton, dan tegangan tarik terutama ditahan oleh batang baja, yang bersama-sama membentuk rangka. Sumbu l – (horizontal) dan t – (vertikal) masing-masing merujuk pada orientasi batang baja longitudinal dan transversal. Sudut penopang beton, θ c , bergantung pada tegangan baja yang dioles ρ l f l dan ρ t f t pada arah l – dan t – 50 bersama dengan tegangan yang dibawa oleh serat. Di sini, ρ l dan ρ t adalah rasio tulangan, di mana ρ l adalah total luas tulangan pada arah longitudinal anggota dibagi dengan keliling garis tengah aliran geser dikalikan dengan ketebalan tabung (yaitu, ρ l = A st /( u o t d )), dan ρ t adalah luas tulangan melintang pada satu dinding sisi tabung dikalikan dengan jarak tulangan (yaitu, ρ t = As w /( t d s )), seperti yang ditunjukkan pada Gambar 1 , dan fl dan f t adalah tegangan pada tulangan memanjang dan melintang, masing – masing. Untuk model plastis penuh dari penampang persegi panjang pada batas batas ultimit, dan asalkan penghancuran web tidak terjadi sebelum leleh pada tulangan arah l dan t , torsi yang ditentukan tentang sumbu l harus sama dengan yang dari sumbu t (yaitu T l = T t ) dan, oleh Persamaan (3), nilai θ c pada ultimit ( θ cu ) adalah:
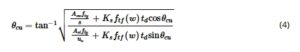
di mana f ly dan f ty adalah kekuatan luluh tulangan pada arah l dan t , berturut-turut. Untuk anggota tanpa serat, Persamaan ( 4 ) diselesaikan secara langsung; namun, jika serat digunakan, diperlukan prosedur iteratif. Ketika kapasitas baja longitudinal dan baja melingkar sama (yaitu, ρ l f l = ρ t f t ) maka dari Persamaan ( 4 ) θ cu = 45°, apakah serat disertakan atau tidak.
Walaupun secara mekanis sudut θ cu pada Persamaan ( 4 ) tidak memiliki batasan teoritis, namun dibatasi oleh kapasitas medan tegangan untuk berputar dari sudut pada retak ( θ cr ) ke sudut pada titik ultimit ( θ cu ). Hal ini dibahas lebih rinci pada Bagian 6.4 , di bawah.
2.3 Perilaku penampang di bawah torsi murni dengan peningkatan beban
Pada penerapan awal serangkaian gaya yang menginduksi tegangan torsional pada suatu penampang, penampang tersebut awalnya berperilaku elastis; pada tahap ini, θ c ≈45°. Setelah retak, baja tulangan menahan tegangan tarik pada retakan dan tegangan tarik pada beton berkurang. Jika beton tidak gagal dalam kompresi, arah retak tetap relatif stabil dan gaya pada baja longitudinal dan hoop terus meningkat. Pada tahap pembebanan ini, sudut penyangga tetap sekitar 45°. Ketika baja pada arah yang diperkuat dengan lemah (longitudinal atau transversal) luluh, gaya internal terus mendistribusikan ulang untuk menyeimbangkan beban yang diberikan hingga kegagalan terjadi dengan luluhnya baja pada arah lain atau penghancuran penyangga diagonal beton. Pada tahap ini, θ c meningkat atau menurun dari 45°, tergantung pada arah baja yang luluh terlebih dahulu; jika tulangan arah t luluh sebelum tulangan arah l , yang biasanya terjadi, θ c <45°, jika tidak θ c ≥45°. Tahap akhir terjadi ketika baja luluh ke arah lain atau beton hancur. Pada tahap ini, arah tegangan utama berhenti berputar, dan kapasitas ultimit tercapai.
2.4 Kapasitas dibatasi oleh penghancuran web
Dengan mempertimbangkan setiap dinding tabung sebagai membran, teori medan kompresi termodifikasi (MCFT) yang dikembangkan oleh Vecchio dan Collins 51 dapat digunakan untuk menentukan kapasitas penyangga. Dalam pendekatan ini, kekuatan beton yang retak dalam kompresi merupakan fungsi dari regangan tarik utama yang ada bersamaan dalam beton.
Menurut pendekatan MCFT, sebagaimana diterapkan pada membran yang dibentuk oleh dinding tabung ekuivalen, untuk menghindari penghancuran jaringan, kapasitas torsi dibatasi pada:
![]()
di mana f cm adalah kekuatan tekan rata-rata silinder beton, dan β adalah faktor efisiensi penyangga, dan diberikan oleh Collins dan Mitchell 52 sebagai:
![]()
Pada Persamaan ( 6 ), regangan tarik utama ε 1 diperoleh dari kondisi kompatibilitas. Yaitu, hubungan antara tiga tegangan bidang ( f l , f t , dan τ lt ) dengan tiga regangan bidang ( ε l , ε t , dan γ lt ) digunakan untuk menentukan regangan utama ( ε 1 dan ε 2 ) yang selanjutnya menentukan kapasitas penyangga.
Kompatibilitas mensyaratkan bahwa, secara rata-rata, deformasi pada beton harus sama dengan deformasi pada tulangan. Dengan demikian, setiap perubahan regangan beton akan disertai dengan perubahan regangan baja yang sama. Yaitu:
![]()
di mana ε sl , ε st adalah regangan pada baja dan ε cl , ε ct adalah regangan pada beton dalam arah l dan t , berturut-turut. Jika tiga komponen regangan ε l , ε t , dan γ lt diketahui, maka regangan pada arah lain dapat ditemukan dari invarian regangan pertama:
![]()
di mana ε 1 adalah regangan tarik utama dan ε 2 adalah regangan tekan utama. Sudut kemiringan regangan utama θ ε terhadap sumbu x ditemukan menggunakan lingkaran Mohr sebagai berikut:
![]()
Regangan pada beton dan baja tulangan bergantung pada hubungan antara sudut θ ε dan θ c . Seperti dibahas di atas, untuk ρ l f l = ρ t f t , θ c = 45°, sedangkan untuk ρ l f l > ρ t f t , θ c < 45° dan ρ l f l < ρ t f t , θ c >45°. Dengan mempertimbangkan situasi di mana tulangan longitudinal dan tulangan melingkar meleleh sebelum terjadi penghancuran, kita dapat mengganti ε l = ε ly dan ε t = ε ty ke dalam Persamaan ( 8 ) dan nilai ε 1 pada titik di mana arah kedua (kritis) meleleh dapat diperoleh dari salah satu berikut ini:
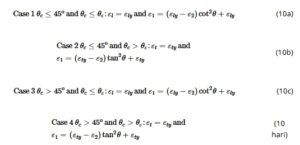
di mana θ adalah sudut regangan utama. Perlu dicatat bahwa dalam kasus ini regangan pada tulangan arah l atau t sama dengan regangan luluhnya, sementara yang lain sama dengan atau lebih besar dari regangan luluhnya dan, karena tulangan longitudinal dan hoop keduanya mengalami leleh (yang diinginkan). Memperhatikan bahwa untuk pendekatan model retak putar MCFT, sudut regangan utama sama dengan sudut tegangan utama dan mengadopsi nilai θ = θ c dalam Persamaan (10) untuk digunakan dalam Persamaan ( 5 ), model tersebut memberikan batas bawah yang konservatif untuk kapasitas penyangga. Tegangan pada suatu titik untuk elemen membran R-SFRC dapat direpresentasikan oleh lingkaran tegangan Mohr, seperti yang ditunjukkan pada Gambar 2 .
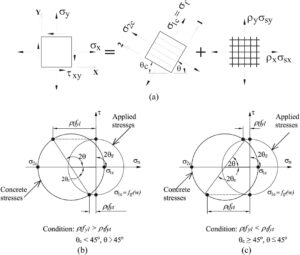
3 KONTRIBUSI SERAT BAJA TERHADAP KEKUATAN TORSIONAL R-SFRC
3.1 Pendahuluan
Jarang sekali pengujian kontrol dilakukan untuk menentukan sifat dasar material pada balok R-SFRC yang diuji dalam torsi, baik secara langsung maupun tidak langsung. Sifat kekuatan tarik sisa SFRC diperlukan untuk input ke dalam persamaan desain dan, dengan demikian, diperlukan model untuk menentukan sifat beton serat pascaretak. Beberapa model tersedia dalam literatur; misalnya, persamaan empiris berdasarkan volume serat untuk memprediksi hasil uji tekukan prisma, seperti yang dilakukan Moraes et al., 53 dikombinasikan dengan prosedur analisis invers 9 ; model analitis didasarkan pada pengamatan fisik-mekanis seperti yang dilakukan Lim et al., 27 dengan model ikatan serat-matriks yang sesuai, seperti yang diadopsi oleh Ju et al., 25 atau VEM dari. 54 , 55 , 37 VEM telah terbukti dari waktu ke waktu memberikan perkiraan yang andal mengenai kekuatan sisa anggota SFRC dalam geser untuk berbagai jenis dan volume serat 54 , 56 – 58 dan digunakan di sini.
3.2 Model keterlibatan variabel
Dalam pendekatan VEM, kontribusi serat ditentukan dari:

Karena pengikatan serat secara progresif saat retakan terbentuk, dan proses regangan baja tulangan saat beban meningkat, terdapat lebar retak kritis yang menentukan kontribusi serat. Ada dua kasus yang perlu dipertimbangkan; yang pertama adalah saat lebar retak pada titik saat tulangan longitudinal dan melingkar telah luluh (dengan satu arah atau lainnya lebih kritis, tergantung pada rasio tulangan) lebih kecil dari lebar retakan saat nilai K f , yang ditentukan oleh Persamaan ( 12 ), telah mencapai maksimumnya (yaitu, lebar retak yang sesuai dengan dK f / dw = 0). Dalam kasus ini, retakan akan tetap stabil saat tulangan terus meningkat regangannya. Akhirnya, pada titik saat kekuatan serat maksimum tercapai, penampang akan mencapai kapasitasnya dan terjadi kegagalan. Dalam kasus ini, lebar retak pada batas maksimal adalah yang sesuai dengan dK f / dw = 0 dan K f berada pada batas maksimumnya. Kasus kedua yang perlu dipertimbangkan adalah ketika lebar retakan pada titik di mana tulangan longitudinal dan tulangan melingkar sama dengan atau lebih besar dari regangan lelehnya (yang kritis adalah arah kedua untuk leleh) berada pada sisi menurun dari kurva tegangan-retak yang diperoleh dari Persamaan ( 11a-12 ) dan ( 12 ). Dalam kasus ini, kegagalan sesuai dengan titik di mana baja meleleh pada arah kedua yang kritis, dan w adalah lebar retakan pada titik ini. Tegangan pada suatu titik diberikan dalam lingkaran Mohr pada Gambar 2 .
3.3 Lebar retak pada batas kekuatan
Lebar retakan pada kondisi batas kekuatan dapat ditentukan menurut model yang ditetapkan oleh Kaufmann et al. 60 untuk membran SFRC. Model ini merupakan perluasan dari model membran retak Kaufmann dan Marti, 61 dengan penyertaan serat. Dalam pendekatan ini lebar retakan diberikan oleh:

Dalam menentukan f tf ( w ) dari Persamaan (11), nilai maksimum w dan w o diambil sebagai lebar retak pada kondisi maksimal.
4 sTM UNTUK MENGHITUNG KAPASITAS MOMEN TORSIONAL BALOK SFRC
Dengan sTM yang dijelaskan pada Gambar 1 , dan dengan asumsi (1) bahwa kekuatan bagian yang retak lebih besar daripada bagian yang tidak retak dan (2) penghancuran web tidak terjadi sebelum tulangan pada arah l dan t meleleh, sudut θ c ditentukan dari Persamaan ( 4 ) dan kapasitas momen torsi ( T u ) ditentukan dari Persamaan (3), dengan mencatat bahwa T u = T l = T t . Meskipun tidak ada batasan teoritis pada sudut penyangga θ c , permintaan daktilitas memaksakan batasan praktis. Oleh karena itu, sudut penyangga dianggap berada dalam batas untuk θ c ,lower ≤ θ c ≤ θ c ,upper , dalam hal ini T u = min( T l , T t ). Batas θ c ,lower dan θ c ,upper dibahas secara rinci di Bagian 6.4 .
Kapasitas torsi balok R-SFRC tidak boleh kurang dari kekuatan retak torsinya ( T cr ), yang diambil seperti yang ditentukan oleh AS3600 19 :
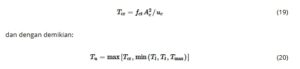
di mana batas penghancuran web, T max , diberikan oleh Persamaan ( 5 ) dan T cr oleh Persamaan ( 19 ).
Proses penyelesaian untuk menghitung kapasitas momen torsi untuk balok SFRC menggunakan sSp-TM adalah sebagai berikut:
- Langkah 1: hitung A c , u c , t d (Persamaan ( 3 )), A o , u o , ρ l , ρ t .
- Langkah 2: asumsikan w = 1,0 mm dan hitung f tf ( w ) menggunakan Persamaan (11) sebagai perkiraan pertama.
- Langkah 3: hitung estimasi pertama θ c menggunakan Persamaan ( 4 ) dengan mengambil sin θ c = cos θ c = 0,707. Hitung ulang θ c menggunakan Persamaan ( 4 ) dengan iterasi.
- Langkah 4: hitung s rf menggunakan Persamaan ( 13-16 ).
- Langkah 5: hitung ε 1 menggunakan Persamaan (10).
- Langkah 6: hitung w baru menggunakan Persamaan ( 17 ) dan hitung w o menggunakan Persamaan ( 18 ). Mengambil nilai maksimum dari w dan w o untuk menghitung f tf ( w ) dengan Persamaan (11).
- Ulangi langkah 3–6 hingga konvergen (ambil nilai konvergen terakhir θ c dari iterasi sebelumnya sebagai estimasi awal untuk θ c ).
- Langkah 7: hitung T l dan T t (Persamaan (3)), T cr (Persamaan ( 19 )) dan T max (Persamaan ( 5 )).
- Langkah 8: hitung kekuatan torsi ( T u ) dengan Persamaan ( 20 ).
5 MODEL RANGKA PUTAR YANG DISEDIAKAN DENGAN SUDUT PUTAR UNTUK MENGHITUNG KAPASITAS MOMEN TORSIONAL BALOK SFRC
Hsu 33 dan Hsu dan Mo 62 mempertimbangkan efek pelunakan penyangga beton diagonal dan mengembangkan model rangka batang yang dilunakkan dengan sudut putar (RA-STM) untuk menentukan kekuatan geser dan torsi anggota RC.

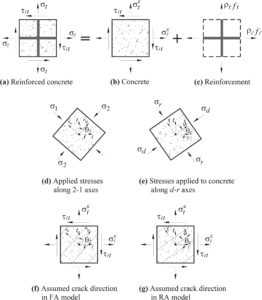
RA-STM mengasumsikan bahwa retakan miring pada sudut putar mengikuti tegangan utama beton pascaretak. Meskipun dapat menangkap riwayat deformasi beban, ia tidak dapat memprediksi kontribusi beton. Untuk mempertimbangkan kontribusi beton, Pang dan Hsu 63 mengembangkan STM yang mengasumsikan bahwa retakan mengikuti dua arah (Gambar 3f ). Model ini, yang didasarkan pada konsep retakan yang diolesi, disebut model rangka baja sudut tetap yang dilunakkan (FA-STM). Perbedaan antara sudut θ 2 dan θ c adalah sudut deviasi. FA-STM dapat memperhitungkan sudut deviasi antara arah retakan utama dan awal yang tetap. 63 , 64
Banyak penelitian telah mengadopsi pendekatan FA-STM dalam analisis torsional mereka. Baru-baru ini, Ju et al. 25 , 65 menerapkan FA-STM untuk mengembangkan model perilaku torsional SFRC. Meskipun model mereka memberikan estimasi yang baik tentang kekuatan torsional balok R-SFRC, model tersebut mengikuti proses iterasi yang membosankan, sehingga kurang cocok untuk dimasukkan dalam kode desain.
Dalam studi ini, Hsu 33 RA-STM disederhanakan (sRA-STM) dengan semua persamaan yang mengatur berasal dari persyaratan dasar keseimbangan, kompatibilitas, dan hubungan material. Untuk kasus torsi murni, hubungan ini disajikan dalam Tabel 1 ; untuk latar belakang derivasinya lihat Hsu, 33 di mana k 1 = rasio tegangan rata-rata terhadap tegangan puncak; ε ο = regangan beton yang tidak dilunakkan pada tegangan maksimum; ε d , ε r = regangan utama rata-rata dalam arah d dan r ; ε ds = regangan maksimum pada permukaan beton; ζ = koefisien pelunakan beton; σ d , σ r = tegangan utama dalam arah d dan r , masing-masing.
| 1. Persamaan keseimbangan | σl=σdcos2θc+σrsin2θc+ρlfl=0 | (1.1) |
| σt=σdsin2θc+σrcos2θc+ρtft=0 | (1.2) | |
| τlt=(σd−σr)sinθccosθc | (1.3) | |
| Tu=2A0q=2Aotdτlt | (1.4) | |
| 2. Persamaan kompatibilitas | εl=εdcos2θc+εrsin2θc | (1.5) |
| εt=εdsin2θc+εrcos2θc | (1.6) | |
| εd=εds/2 | (1.7) | |
| 3. Hubungan konstitutif | fl=fly… untukεl≥εly | (1.8a) |
| fl=Esεl… untukεl<εly | (1.8b) | |
| 3.a. Penguatan | ||
| ft=fty… untukεt≥εty | (1.9a) | |
| ft=Esεt… untukεt<εty | (1.9b) | |
| 3.b. Beton dalam tekanan | σd=ζk1fc′ | (1.10) |
| ζ=εd(1−μ)εd−εr | (1.11) | |
| k1=(εdsζεo)−13(εdsζεo)2…for|εds|≤|ζεo| | (1.12a) | |
| k1=[1−ζ2(2−ζ)2](1−13ζεoεds)+ζ2(2−ζ)2εdsζεo(1−13εdsζεo)…for|εds|>|ζεo| | (1.12b) | |
| 3.c. Beton dalam tarikan | σr=Ecεr…forεr≤εcr | (1.13a) |
| σr=0,(RC)σr=Ksftf(w),(R−SFRC)]…forεr>εcr | (1.13b) | |
| 4. Rata-rata regangan utama dalam arah r | εr=−(σd+ρtEsεd)tan2θc−Ksftf(w)ρtEs…forεt<εyt | (1.14) |
Penyederhanaan berikut diterapkan pada model ini:
- Persamaan ( 2 ) digunakan untuk menghitung tebal dinding tabung ekivalen ( t d );
- Kontribusi serat baja ditambahkan dalam Persamaan (1.13b) pada Tabel 1 menggunakan Persamaan (11) seperti yang dijelaskan di atas. Untuk penyederhanaan, K f ,max diterapkan menggunakan Persamaan ( 21 ) seperti yang diberikan dalam Voo et al. 58 :

- Sudut penyangga kompresi θ c dihitung menggunakan Persamaan ( 4 ).
Proses iterasi Hsu 33 digunakan untuk memperoleh solusi untuk sRA-STM yang diusulkan:
- Langkah 1: hitung A c , u c , t d (Persamaan (3)), A o , u o , ρ l , ρ t .
- Langkah 2: hitung f tf (w) menggunakan Persamaan (11).
- Langkah 3: pilih ε ds = 0,003 dan ε d = ε ds /2.
- Langkah 4: asumsikan nilai ε r .
- Langkah 5: hitung σ d dari Persamaan (1.10)–(1.12) pada Tabel 1 .
- Langkah 6: hitung θ c awal menggunakan Persamaan ( 4 ) dengan mengambil sin θ c = cos θ c = 0,707. Hitung ulang θ c menggunakan Persamaan ( 4 ) dengan iterasi.
- Langkah 7: hitung ε l dari Persamaan (1.5) dan ε t dari Persamaan (1.6) pada Tabel 1 .Jika ε t ≥ ε ty dan ε l ≥ ε ly , pilih nilai baru untuk ε r , ulangi langkah 4–7 sampai Persamaan (1.2) pada Tabel 1 terpenuhi; ataujika ε t < ε ty , dan ε l < ε ly atau ε l ≥ ε ly hitunglah ε r , baru dari Persamaan (1.14) pada Tabel 1 . Pilih nilai baru untuk ε r . Hitung ulang θ c menggunakan Persamaan ( 4 ) dengan mengganti f ty dengan f t ( f t = E s ε t ) dan fly dengan fl ( f l = E s ε l ) atau fly .
- Langkah 8: Ulangi langkah 4–7 hingga ε r menjadi sama dengan ε r yang dihitung dari Persamaan (1.14) pada Tabel 1 .
- Langkah 9: hitung τ dari Persamaan (1.3) pada Tabel 1 dengan mengambil σ r = f tf (w) dan kemudian hitung T u dari Persamaan (1.4) pada Tabel 1 .
6 PROGRAM EKSPERIMENTAL
6.1 Variabel dan dimensi spesimen
Sebuah penyelidikan eksperimental dilakukan pada total enam balok yang mengalami torsi murni. Salah satu spesimen diperkuat dengan tulangan batang baja konvensional tanpa serat (spesimen kontrol), sementara lima spesimen diperkuat dengan serat baja, dengan atau tanpa jumlah tulangan lingkaran batang yang berbeda di zona pengujian. Semua anggota secara geometris identik, dengan panjang keseluruhan 6300 mm, penampang melintang 250 × 450 mm (lihat Gambar 4 ), dan penutup bening ke bagian luar tulangan lingkaran (sengkang tertutup) sebesar 15 mm. Spesimen berisi batang tulangan baja deformasi longitudinal berdiameter 16 mm (N16); di mana batang lingkaran disediakan, diameter batang adalah 10 mm (N10). Kedalaman efektif dari serat ekstrem ke pusat tulangan longitudinal terjauh adalah d = 417 mm.

Semua balok terdiri dari daerah uji, di mana torsi murni diasumsikan berkembang sepenuhnya, dan dua daerah terganggu yang terletak di setiap ujung anggota (lihat Gambar 4 ). Untuk mencegah kegagalan torsi serta kerusakan lokal karena konsentrasi tegangan dan untuk mendorong perkembangan penuh kegagalan torsi di bagian tengah balok (yaitu, di dalam daerah yang dipantau), daerah terganggu luar dilengkapi dengan sengkang berdiameter 10 mm yang berjarak dekat (jarak = 100 mm) dan tulangan longitudinal tambahan.
Tata nama spesimen mengikuti format TX-Y y -Db-S, di mana X adalah nomor spesimen dalam urutan yang diuji (1–6), Y = PC untuk anggota tanpa serat dan Y = SFRC untuk anggota dengan serat, dengan y sama dengan dosis nominal (30 atau 60 kg/m 3 ), dan Db dan S masing-masing mewakili diameter dan jarak tulangan melintang (batang) (jika tidak menggunakan tulangan melintang, Db-S = 0). Dengan mempertimbangkan notasi ini, spesimen T1-PC-10/200 adalah balok beton polos (PC) dan berisi sengkang baja deformasi berdiameter 10 mm yang diberi jarak 200 mm c/c di dalam zona uji. Tiga balok SFRC (T2-SFRC30-10/200, T3-SFRC30-10/400, dan T4-SFRC30-0) diperkuat dengan 30 kg/m 3 serat baja. Balok T2-SFRC30-10/200 dan T3-SFRC30-10/400 berisi sengkang baja deformasi berdiameter 10 mm yang diberi jarak masing-masing 200 dan 400 mm. Dosis serat untuk balok T5-SFRC60-10/400 dan T6-SFRC60-0 adalah 60 kg/m 3 . Sengkang baja berdiameter 10 mm digunakan pada T5-SFRC60-10/400 dengan jarak 400 mm. Susunan tulangan melintang dipilih berdasarkan balok T1-PC-10/200 dan T2-SFRC30-10/200 yang diperkuat dengan tulangan melintang minimum yang diperlukan ( A sv.min ) yang direkomendasikan oleh AS3600, 19 sementara balok T3-SFRC30-10/400 dan T5-SFRC60-10/400 mengandung setengah dari rasio tulangan melintang minimum yang diperlukan. Tidak ada tulangan baja melintang yang ditempatkan pada balok T4-SFRC30-0 dan T6-SFRC60-0.
6.2 Sifat material
PC dibuat dari rancangan campuran komersial dengan ukuran agregat maksimum 10 mm, kemerosotan 150 mm, dan kuat tekan nominal 28 hari sebesar 32 MPa. Spesimen tanpa serat dituang terlebih dahulu, kemudian jumlah serat baja yang dibutuhkan ditambahkan ke PC dan dicampur dalam pengaduk selama minimal 10 menit sebelum pengecoran spesimen SFRC. PC dipadatkan menggunakan vibrator poker; spesimen SFRC dipadatkan menggunakan vibrator eksternal yang dipasang di sisi bekisting untuk memastikan distribusi serat yang merata.
Spesimen dicetak dalam dua tuangan. Spesimen PC T1-PC-10/200 dicetak pada tuangan pertama, diikuti oleh balok SFRC (T2-SFRC30-10/200, T3-SFRC30-10/400 dan T4-SFRC30-0) dengan 30 kg/m3 serat baja (Gelombang 1). Spesimen T5-SFRC60-10/400 dan T6-SFRC60-0 dicetak pada tuangan kedua (Gelombang 2) dengan 60 kg/m3 serat baja. Setelah pengecoran, spesimen ditutup dengan kain goni basah dan lembaran plastik. Spesimen diawetkan dengan metode basah selama 28 hari, setelah itu spesimen dibersihkan, dikeringkan, dan diukur sebelum pengujian.
Selama pengecoran spesimen SFRC, tiga silinder berdiameter 150 mm dan tinggi 300 mm dikumpulkan pada awal, tengah, dan akhir penuangan untuk menentukan dosis serat baja yang tepat. Serat diekstraksi dari campuran beton menggunakan magnet setelah mencuci pasta semen. Serat dikeringkan sebelum ditimbang. Untuk Batch 1, dosis rata-rata yang diukur pada awal, tengah, dan akhir penuangan masing-masing adalah 36,6, 32,8, dan 38,4 kg/m 3 . Untuk Batch 2, dosis serat yang diukur pada awal, tengah, dan akhir penuangan masing-masing adalah 59,7, 64,3, dan 54,7 kg/m 3 . Dosis serat target adalah 30 dan 60 kg/m 3 untuk Batch 1 dan Batch 2. Serat baja Dramix 5D 65/60 ujung kait memiliki panjang 60 mm dan diameter 0,9 mm serta memiliki kekuatan tarik pamungkas 2300 MPa.
Untuk menentukan sifat material PC dan SFRC, sampel silinder pendamping, tulang anjing, dan prisma juga dicetak bersama spesimen balok. Sampel pendamping diuji pada hari pengujian spesimen balok masing-masing. Kekuatan tekan rata-rata PC dan kelompok 1 dan 2 SFRC masing-masing adalah 38,6, 45,6, dan 37,5 MPa.
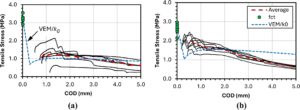
Sifat mekanik jangka pendek yang diukur dari spesimen PC dan SFRC dirangkum dalam Tabel 2 dan 3. Sifat fraktur SFRC ditentukan secara langsung dengan mendapatkan kuat tarik matrik beton f ct , dan kuat tarik residual rata-rata, f 1,5 (diambil pada lebar retak 1,5 mm), dari spesimen berbentuk dogbone uniaxial yang diuji menurut prosedur yang diuraikan dalam Lampiran AS3600. 19 COD tegangan penuh (−) diberikan dalam Gambar 5 , bersama dengan prediksi VEM, disesuaikan dengan bias serat. Perlu dicatat bahwa, karena beton dengan slump tinggi digunakan dalam desain campuran, bias serat terjadi pada uji dogbone karena proses pemadatan. Faktor bias serat k 0 = 0,64 diadopsi, sesuai dengan rekomendasi Kode Model serat 2020. 66 Diamati bahwa VEM memberikan perkiraan yang wajar dari kurva σ – w untuk lebar retak pada spesimen 30 kg/m 3 , dan untuk lebar 3,0 mm atau kurang pada spesimen 60 kg/m 3 . Untuk lebar retak lebih besar dari 3,0 mm, model tersebut melebih-lebihkan kekuatannya. Sifat tarik juga ditentukan secara tidak langsung dari kekuatan lentur sisa melalui prisma berlekuk dan tidak berlekuk yang diuji menurut EN 14651 67 dan ASTM C1609, 68 .
| Nomor Batch. | AS3600 19 Tegangan uniaksial | EN 14651 67 Uji tekuk prisma | Uji tekuk prisma ASTM C1609 (2006) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| fct[MPa] | f1.5[MPa] | fR1[MPa] | fR2[MPa] | fR3[MPa] | fR4[MPa] | fP[MPa] | f1[MPa] | f600D[MPa] | f150D[MPa] | |
| #1 | 3.21 | 1.23 | 3.25 | 4.70 | 4.05 | 3.19 | 5.8 | 5.5 | 3.5 | 5.1 |
| # Nomor 2 | 2.63 | 1.61 | 4.31 | 5.85 | 6.14 | 5.10 | 7.8 | 5.5 | 4.5 | 6.8 |
| Contoh | f cm | dari 1.5 | E -mail | T cr | ( GJ ) dia | T maks | ϕ / L pada T maks | θ cr pada T maks a |
|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (GPa) | (kNm) | kNm 2 | (kNm) | (rad/m2) | (derajat) | |
| T1-PC-10/200 | 38.6 | – | 30.9 | 25.1 | 23,5 × 10 103 | 46.9 | 0,0342 | 40,9–50,8 (46,3) |
| T2-SFRC30-10/200 | 45.6 | 1.23 | 32.6 | 28.1 | 21,7 × 10 3 | 72.5 | 0,0372 tahun | 42.1–50.3 (46.3) |
| T3-SFRC30-10/400 | 45.6 | 1.23 | 32.6 | 21.9 | 20,7 × 10 103 | 46.2 | 0,0363 tahun | 36,4–43,5 (40,3) |
| T4-SFRC30-0 | 45.6 | 1.23 | 32.6 | 23.5 | 20,2 × 10 3 | 31.9 | 0,0125 | 38,0–50,3 (45,8) |
| T5-SFRC60-10/400 | 37.5 | 1.61 | 30.9 | 21.2 | – B | 46.5 | 0,0379 pukul 0,0379 | 39,3–49,0 (44,4) |
| T6-SFRC60-0 | 37.5 | 1.61 | 30.9 | 22.5 | 21,5 × 10 3 | 34.6 | 0,0132 | 38.3–48.2 (42.7) |
Kisaran sudut retakan yang terletak sepenuhnya dalam zona pengujian, dengan rata-rata ditunjukkan pada (). b Pengukuran kekakuan elastis untuk Spesimen T5 tidak dianggap andal karena inklinometer lengket pada perpindahan rendah.
Kandang penguat spesimen disiapkan dengan batang baja deformasi nominal 500 MPa. Kekuatan luluh rata-rata terukur dari batang N10 (Daktilitas normal, diameter 10 mm) dan N16 (Daktilitas normal, diameter 16 mm) masing-masing adalah 582 dan 579 MPa. Modulus elastisitas rata-rata terukur dari batang N10 dan N16 masing-masing adalah 203 dan 194 GPa.
6.3 Pengaturan dan instrumentasi eksperimen
Susunan pengujian ditunjukkan pada Gambar 6 dan 7. Semua spesimen balok diuji menggunakan dua aktuator Instron berkapasitas 500 kN yang ditopang oleh rangka pengujian yang kaku (Gambar 6 ), dengan torsi yang diberikan melalui gaya eksentrik yang diterapkan pada lengan penyangga. Rentang antara penyangga adalah 4400 mm, dan lengan tuas torsi pada setiap penyangga balok untuk beban awal adalah 813 mm (Gambar 7 ).

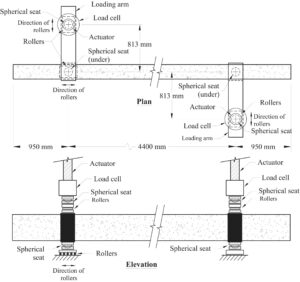
Saat balok terpelintir, lengan tuas dari beban yang diberikan berkurang. Untuk mengakomodasi gerakan ini, rol dan dudukan bulat ditempatkan di antara aktuator dan lengan pemuatan, memastikan bahwa beban tetap vertikal, dengan demikian mencegah tegangan lentur pada piston hidrolik aktuator (Gambar 7 ). Pengurangan pada lengan tuas diukur secara terus-menerus selama pengujian menggunakan transduser diferensial variabel linier kawat tarik saat perpindahan yang diberikan meningkat, dan pengukuran ini disertakan dalam perhitungan torsi yang diberikan. Dukungan terletak di bagian bawah balok; satu dukungan (ujung utara) memiliki rol dan dudukan bulat untuk memungkinkan gerakan rotasi dan translasi bebas, sedangkan dukungan lainnya (ujung selatan) memiliki dudukan bulat untuk memungkinkan gerakan rotasi bebas tentang sumbu longitudinal balok.
Selain itu, setiap spesimen dilengkapi dengan empat inklinometer, dua di setiap lengan penyeimbang, untuk merekam sudut puntir. Untuk mendeteksi potensi pembentukan retakan, lima pengukur regangan beton dipasang di bagian tengah balok. Korelasi citra digital (DIC) digunakan untuk terus memantau pertumbuhan retakan di dalam zona pengujian. Pengukur regangan juga dipasang pada batang baja terpilih untuk menentukan beban leleh. Aktuator dikontrol menggunakan perpindahan ram pada kecepatan 1,5 mm/menit (setara dengan 0,1°/menit) hingga kerusakan signifikan di luar kegagalan atau rotasi 12°, mana yang terjadi lebih dulu. Batas yang ditetapkan pada rotasi maksimum absolut adalah untuk memastikan bahwa dudukan bulat tidak berputar melampaui batasnya dan terkunci.
6.4 Hasil Eksperimen

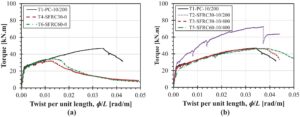
Spesimen tanpa sengkang (T4-SFRC30-0 dan T6-SFRC60-0) menunjukkan pengerasan torsional setelah retak mirip dengan balok PC hingga (0,012 rad/m), diikuti oleh cabang menurun (Gambar 8a ). Meskipun tidak adanya tulangan melintang, balok T4-SFRC30-0 dan T6-SFRC60-0 menunjukkan beberapa tingkat daktilitas, meskipun secara signifikan lebih rendah daripada spesimen kontrol (sekitar sepertiga dari kontrol). Juga dicatat bahwa dosis serat yang lebih tinggi (dari 30 hingga 60 kg/m 3 ) memiliki dampak yang dapat diabaikan hingga sedikit pada kapasitas torsional.
Balok RC dan balok R-SFRC yang diperkuat dengan 50% sengkang dari balok PC (T3-SFRC30-10/400 dan T5-SFRC60-10/400) menunjukkan kinerja kekuatan dan daktilitas yang serupa dengan uji kontrol (Gambar 8b ). Serat baja mempertahankan penampang balok selama pengujian dan tidak ada penutup yang terkelupas. Ini memperkuat pengamatan bahwa sebagian tulangan melintang dapat diganti dengan serat baja. Spesimen T2-SFRC30-10/200 dengan 30 kg/m 3 serat sebagai tambahan tulangan melintang minimum kode menunjukkan peningkatan kekuatan yang signifikan (+55%) dibandingkan dengan kontrol.
Selama pengujian, perkembangan regangan beton permukaan dan pola retak terus dipantau di dalam zona pengujian menggunakan pemantauan DIC. Nilai regangan dan pola retak, di dalam zona pengujian, pada beban puncak, ditunjukkan pada Gambar 9 dan disediakan dalam Tabel 3 , yang memberikan pemahaman yang lebih baik tentang respons torsi-puntir yang diamati dan kapasitas torsi pamungkas balok.

Kasus-I—Balok RC ( ρ f = 0, A sv = A sv,min ): Pola retak balok RC konvensional dengan tulangan melintang, T1-PC-10/200, sebagian besar terdiri dari retakan diagonal/spiral yang muncul setelah beban retak dan menjalar dengan torsi yang diberikan lebih lanjut (Gambar 10 a ). Pada puntiran yang diberikan lebih tinggi, batang tulangan baja mendistribusikan regangan tarik dari daerah retak ke daerah beton yang tidak retak, sehingga mengakibatkan terbentuknya retakan sekunder di antara retakan yang sudah ada. Pembentukan retak progresif ini pada sudut puntiran yang lebih besar mengakibatkan pola retak menyebar di seluruh zona pengujian tanpa kerusakan lokalisasi yang signifikan dan menghadirkan ketahanan torsi yang lebih tinggi dengan meningkatnya sudut puntiran. Respon torsi dan pola retak yang diamati konsisten dengan yang dilaporkan dalam literatur untuk balok RC.
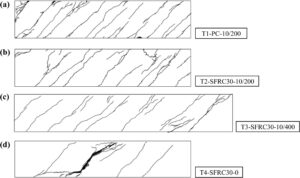
Kasus-II—Balok SFRC ( ρ f >0, A sv = 0): Sebaliknya, untuk balok SFRC tanpa sengkang (T4-SFRC30-0 dan T6-SFRC60-0), semua retakan berkembang dan stabil sebelum dimulainya cabang menurun pasca-puncak dari respons torsi-puntir (Gambar 10d ). Untuk spesimen T4-SFRC30-0, retakan diagonal kritis berkembang pada muka Barat, dan tidak merambat terus menerus dalam pola spiral sepanjang balok seperti yang diamati pada Kasus-I (Gambar 10d ). Sebaliknya, retakan melebar di seluruh lebar balok. Demikian pula, retakan diagonal kritis berkembang pada muka Timur (Gambar 9d ) dan terus tumbuh di seluruh lebar balok hingga muncul di muka Barat (muka DIC). Dengan demikian, pada balok SFRC tanpa sengkang, kegagalan terjadi saat kerusakan terlokalisasi pada satu retakan kritis, yang mengakibatkan peningkatan progresif pada lebarnya, yang, tidak seperti balok RC (Kasus I), berhubungan dengan pengurangan resistansi torsi pada sudut puntir yang lebih tinggi (lihat Gambar 8 ).
Kasus-III—Balok R-SFRC ( ρ f >0, A sv >0): Untuk balok dengan serat baja dan tulangan melintang, perilakunya menyerupai kombinasi Kasus I dan II. Pada dosis serat yang rendah, kapasitas torsi dan daktilitas R-SFRC dengan 50% tulangan geser minimum ( A sv = 0,5 A sv,min ) mirip dengan balok RC, seperti yang terlihat pada Gambar 8. Pada A sv,min penuh , peningkatan signifikan dalam kapasitas torsi dicapai untuk dosis serat yang kecil.
Pola retak balok R-SFRC juga muncul sebagai kombinasi Kasus I dan II. Beberapa retakan terbentuk pada torsi retak, seperti pada Kasus I, yang menyebar untuk menyambung secara spiral pada beban yang lebih tinggi. Retakan sekunder terbentuk pada sudut puntir yang lebih tinggi. Seperti Kasus II, salah satu retakan awal berkembang sebagai retakan kritis yang mengalami pelebaran lebih lanjut dan kerusakan lokal. Perilaku keseluruhan terletak di antara balok RC tanpa serat (Kasus I) dan balok R-SFRC (Kasus II). Dengan pengurangan tulangan geser, lebih sedikit retakan yang terbentuk dengan jarak yang lebih besar di antara retakan, yang mengakibatkan peningkatan lokalisasi pada retakan dan pelebaran progresif dari satu atau lebih retakan kritis (lihat Gambar 9c dan 10c ).
Dua pengamatan utama mengenai orientasi retak juga dicatat. Pertama, karena kegagalan balok SFRC berlanjut melalui pelebaran retakan kritis yang sudah stabil pada tahap retak awal, retakan kritis kemungkinan berada pada sudut yang lebih besar daripada sudut regangan utama pada puntiran yang diterapkan lebih tinggi. Misalnya, untuk balok T4-SFRC30-0, retakan kritis berada pada sekitar 47,5°. Perpanjangan yang terbentuk di tepi atas dan bawah balok terbentuk selanjutnya. Perpanjangan tersebut lebih datar, kemungkinan karena adanya tulangan longitudinal. Kedua, sementara beberapa rotasi retakan (indikasi rotasi medan regangan) diamati, rentang rotasi retakan kecil hingga torsi puncak (kira-kira 5–10°). Selain itu, sudut retakan tidak mendatar melebihi 28° seperti yang diamati dalam estimasi teoritis. Oleh karena itu, disarankan untuk membatasi orientasi retakan guna memastikan batas permintaan duktilitas terpenuhi.
Keterbatasan pada variasi maksimum sudut penopang beton dari kondisi elastis untuk geser dan torsi, serta untuk elemen seperti membran dan cangkang, telah lama dikenal. Misalnya, Kode Model CEB-FIP 1990 69 menetapkan batas bawah 18,4° (cot θ = 3,0) pada sudut antara penopang dan sumbu longitudinal anggota, sedangkan edisi Eurocode 2 70 tahun 2004 menetapkan batas pada θ sebesar 21,8° (cot θ = 2,5). Foster dkk. 71 menyarankan variasi maksimum sebesar 25° dari kondisi elastis (yaitu, sudut minimum sebesar 20° untuk balok RC dalam geser dan torsi).
Baru-baru ini, Kode Model fib 2020 menyarankan batas 15° dari keadaan elastis untuk membran dan cangkang, sedangkan untuk geser dan torsi, batas bawah pada θ didefinisikan sebagai fungsi dari parameter regangan longitudinal tinggi tengah, ε x —ini adalah Tingkat Aproksimasi IIa. Untuk nilai ε x = 0,0025, yang sesuai dengan regangan luluh batang baja 500 MPa dan dengan asumsi semua batang longitudinal (atas dan bawah) luluh bersama-sama dalam kasus torsi murni, ini memberikan batas bawah pada θ sebesar 30° (yaitu, 45° ± 15°). Mengingat pengamatan eksperimental dan temuan dari penelitian sebelumnya, batas 25° ≤ θ ≤ 65° diadopsi dalam analisis berikut. Pengamatan ini menekankan perlunya model yang secara akurat menangkap: (i) mekanika balok RC dalam torsi—model rangka, (ii) keterlibatan dan kontribusi serat, dan (iii) jarak retak dan lebar retak sebagaimana dicapai dalam model yang diusulkan. Pendekatan solusi iteratif yang diusulkan memungkinkan penangkapan aspek-aspek yang disebutkan di atas, interaksinya, dan menghasilkan estimasi kapasitas torsi yang lebih dekat dengan hasil eksperimen dibandingkan dengan model lain yang ada, sebagaimana dijelaskan dalam Bagian 7 .
7 PENILAIAN MODEL
sSp-TM dan sRA-STM yang diusulkan yang dikembangkan di sini diterapkan pada 63 data uji yang dilaporkan dalam literatur (diambil dari Referensi [ 22 , 23 , 25 , 28 , 29 , 32 , 72-74 ] ). Model Amin dan Bentz 22 juga dibandingkan untuk set data yang sama dengan parameter yang dipilih. Ringkasan data eksperimen yang diekstraksi dari literatur diberikan dalam Lampiran II (materi tambahan) untuk makalah ini. Variabel yang dipertimbangkan dalam penelitian ini adalah: kuat tekan beton ( f cm ), rasio tulangan ( ρ l = A st /u o t d dan ρ t = A sw /st d ), fraksi volume serat ( ρ f ), dan rasio aspek serat ( α f ). Karena kuat tarik residual SFRC dari uji lentur prisma tidak tersedia, VEM digunakan untuk memperkirakan kuat tarik pascaretak SFRC. Kapasitas momen torsi yang diukur dari percobaan ( T u .exp ) dibandingkan dengan hasil model, dan kesalahan model (ME) dihitung, di mana ME adalah rasio T u .exp terhadap kekuatan torsi yang ditentukan oleh masing-masing model desain.

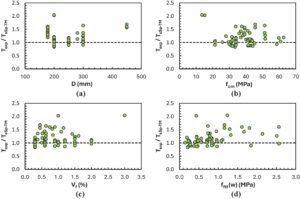
Hasil statistik untuk set data lengkap dan setengah data paling tidak konservatif yang digunakan dalam analisis disajikan dalam Tabel 4 , dengan setengah data paling tidak konservatif juga disajikan pada plot distribusi normal pada Gambar 12. Untuk model sRA-STM dan sSp-TM yang dikembangkan dalam studi ini, diamati bahwa populasi setengah data paling tidak konservatif terwakili dengan baik oleh distribusi normal (lihat Gambar 12 ). Tabel 4 juga menyajikan hasil untuk model terkoreksi Amin dan Bentz, 22 serta untuk model Facconi et al. 34 dan Oettel. 35 Untuk semua model, ketebalan tabung yang diberikan oleh Persamaan ( 2 ) digunakan untuk menentukan kapasitas torsi, dengan parameter lain—seperti kekuatan beton dinding—diambil sesuai yang diadopsi oleh penulis makalah. Seperti disebutkan sebelumnya, sSP-TM yang disajikan dalam makalah ini mirip dengan model Oettel, dengan perbedaan terletak pada bagaimana komponen serat diperlakukan (lihat Bagian 2.2 ). Dalam analisis untuk model Oettel, kapasitas penampang dioptimalkan dengan menentukan sudut θ cu menggunakan Persamaan ( 4 ), tetapi dengan menghilangkan suku sin θ cu dan cos θ cu .
| Model | Data lengkap | Setengah paling tidak konservatif | ||
|---|---|---|---|---|
| Berarti | Virus Corona | Berarti | Virus Corona | |
| sRA-STM | 1.13 | 0.214 | 1.06 | 0.107 |
| sSP-TM | 1.18 | 0.229 | 1.09 | 0.128 |
| Amin dan Bentz 22 | 1.36 | 0.251 | 1.28 | 0,176 tahun |
| Facconi dkk. 34 | 1.38 | 0.239 | 1.28 | 0,125 |
| Oettel 35 | 1.04 | 0.173 | 1.01 | 0.128 |
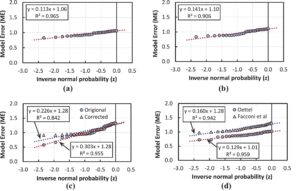
Hasil analisis menunjukkan bahwa model rangka ruang sederhana yang diusulkan (sSp-TM) dan model rangka sudut putar yang disederhanakan (sRA-STM) memberikan korelasi yang baik dengan data eksperimen, dengan tingkat konservatisme yang sesuai. Model rangka ruang Oettel 35 juga menunjukkan korelasi yang sangat baik dengan data uji, meskipun sedikit kurang konservatif karena kontribusi serat yang sama baik dalam arah melintang maupun membujur.
Model Amin dan Bentz 22 dan Facconi et al. (2021) menunjukkan konservatisme yang lebih besar karena nilai tetap untuk θ cu yang diadopsi, dan keterbatasan yang ditimbulkannya pada kemampuan medan tegangan untuk menyesuaikan setelah luluh terjadi di salah satu arah tulangan. Model-model ini dapat ditingkatkan dengan mengadopsi θ cu yang dihitung sebagai batas bawah untuk sudut penyangga dan mengoptimalkan sudut untuk memaksimalkan kontribusi tulangan melingkar. Ini mungkin menjadi penting ketika mempertimbangkan efek gabungan dari torsi, geser, dan tekukan, khususnya ketika kontribusi beton terhadap kapasitas geser dipertimbangkan. Ini adalah topik untuk penelitian mendatang.
8 KESIMPULAN
Dalam studi ini, dua model rangka dikembangkan berdasarkan konsep Rausch 41 dan dikembangkan oleh banyak orang sejak saat itu, termasuk Mitchell dan Collins, 49 Collins dan Mitchell, 44 antara lain, untuk memprediksi kekuatan balok SFRC dalam torsi murni—model rangka ruang sudut tetap (FA-STM) dan model rangka ruang sudut putar yang lebih sederhana (RA-STM), seperti yang dikembangkan oleh Hsu 33 untuk anggota tanpa serat. Dalam makalah ini, pendekatan rasional dikembangkan untuk penyertaan serat dengan sudut penyangga tekan yang dihitung menggunakan analogi rangka ruang dengan pertimbangan yang tepat dari komponen serat—kapasitas komponen serat ditentukan menggunakan VEM. Sudut penyangga tekan dihitung dengan asumsi bahwa setelah baja tulangan meleleh dalam satu arah, retakan bebas berputar hingga leleh terjadi di arah lain, atau beton hancur. Sebelum retak, di bawah kondisi hampir elastis, sudut tegangan tekan utama adalah 45°, yang tetap ada hingga luluh terjadi pada salah satu tulangan longitudinal atau transversal (dengan ketentuan bahwa penghancuran jaring tidak terjadi sebelumnya)—di luar luluh, arah tegangan utama dapat tetap pada 45°, untuk kasus ρ l f l = ρ t f t , atau berputar plus atau minus dari 45° tergantung pada rasio volume-tegangan tulangan longitudinal terhadap transversal ( ρ l f l / ρ t f t ). Ini adalah persyaratan model dan dikonfirmasi oleh hasil pengujian.
Selain pengembangan model, uji torsi murni struktural dilakukan pada enam balok dengan dosis serat dan tulangan geser yang berbeda (termasuk satu spesimen kontrol tanpa serat). Ada perbedaan signifikan yang diamati dalam pola retak dan mekanisme kegagalan balok RC dan R-SFRC. Dalam kasus balok R-SFRC tanpa tulangan lingkaran batang konvensional (sengkang tertutup penuh), sementara beberapa retakan terbentuk dengan peningkatan puntiran (mirip dengan balok RC), pada tahap tertentu salah satu retakan menjadi kritis dan kegagalan berlanjut setelahnya dengan pelebaran retakan kritis. Ini juga memengaruhi rotasi retakan dan daktilitas elemen. Oleh karena itu, model torsi yang dapat diterima untuk R-SFRC harus secara ketat menangkap pengaruh mekanika RC, keterlibatan dan kontribusi serat, dan retak R-SFRC seperti yang dicapai dalam model yang diusulkan dan pendekatan solusi iteratif.
Pengujian menunjukkan bahwa, dengan syarat sekurang-kurangnya 50% dari persyaratan tulangan lingkar minimum dipertahankan dalam bentuk sengkang tertutup penuh (batang), anggota-anggota tersebut mencapai tingkat daktilitas yang sama dengan uji kontrol, bahkan di mana sengkang-sengkang ini diberi jarak yang lebar, seperti pada spesimen T3-SFRC30-10/400 dan T5-SFRC60-10/400, dengan rasio jarak sengkang ( s ) terhadap kedalaman efektif ( d ) sebesar s / d = 0,96. Spesimen tanpa tulangan lingkar (T4-SFRC30-0 dan T6-SFRC60-0) menunjukkan tingkat daktilitas yang jauh lebih rendah daripada kontrol (kira-kira sepertiga dari putaran pada titik ultimit dibandingkan dengan kontrol). Dengan demikian, direkomendasikan agar sekurang-kurangnya 50 persen dari tulangan lingkar torsi minimum disediakan oleh tulangan lingkar (batang) dengan jarak sengkang tidak melebihi 0,75 d .
Terakhir, model rangka yang diusulkan diuji terhadap kumpulan data 63 balok R-SFRC yang diperoleh dari literatur, bersama dengan data dari penelitian ini. Hasil analisis menunjukkan bahwa model rangka ruang sederhana yang diusulkan (sSp-TM) yang dikembangkan dalam penelitian ini dan model rangka sudut putar yang dilunakkan yang disederhanakan (sRA-STM), yang didasarkan pada RA-STM Hsu, 33 memberikan korelasi yang baik dengan data eksperimen, dengan tingkat konservatisme yang sesuai. Model rangka ruang Oettel 35 juga menunjukkan korelasi yang sangat baik dengan data uji, meskipun sedikit kurang konservatif karena kontribusi serat yang sama baik dalam arah melintang maupun membujur. Model Amin dan Bentz 22 dan Facconi et al. (2021) menunjukkan konservatisme yang lebih besar karena keterbatasan yang ditempatkan pada kemampuan medan tegangan untuk menyesuaikan setelah luluh terjadi pada tulangan, baik dalam arah melintang maupun membujur, dan tidak memanfaatkan daktilitas bawaan sistem.
NOTASI
Sebuah c
area yang dibatasi oleh perimeter luar jalur aliran beton
Sebuah angka 0
area yang dibatasi oleh jalur aliran geser
Sebuah oh
area yang dibatasi oleh garis tengah tulangan torsi transversal eksterior
Sebagai
total luas baja longitudinal
Sebuah sw
luas satu kaki baja melintang
B
lebar bagian
D
kedalaman bagian
df
diameter serat
E -mail
modulus elastisitas beton
Apakah itu
modulus elastisitas baja
f cm
kekuatan tekan rata-rata silinder
f ct
kekuatan tarik beton
f l , f t
tegangan baja pada arah l dan t
f tf ( w )
kekuatan tarik sisa SFRC pada lebar retak w
terbang , f sy
kekuatan luluh baja longitudinal
f terima kasih
kekuatan luluh baja transversal
k 1
rasio tegangan rata-rata terhadap tegangan puncak
k ke
faktor ikatan serat
K f
faktor orientasi global serat
K dan
faktor dispersi serat
aku aku
panjang serat
Q
aliran geser
S
jarak tulangan melintang
rf kecil
jarak retak diagonal
informasi lebih lanjut
jarak retak diagonal maksimum teoritis
saya tidak bisa
jarak retak untuk tegangan uniaxial pada arah tulangan l
rtfo terbaru
jarak retak untuk tegangan uniaxial pada arah tulangan t
T , T kamu
kapasitas momen torsi
T l , T t ,
kekuatan torsi yang disumbangkan oleh baja longitudinal dan baja transversal
tanggal lahir
ketebalan dinding setara (ketebalan dinding tabung)
kamu c
perimeter luar penampang beton
kamu atau
perimeter garis tengah aliran geser
kamu h
keliling garis tengah tulangan torsi transversal tertutup
aku
lebar retak normal terhadap panjang retak
apa
Lebar retak kritis
aku aku
parameter pengikatan serat
sebuah f
rasio aspek serat
sebuah
faktor efisiensi strut kompresi
γ lt
regangan geser rata-rata pada dirn l dan t
aku di
regangan beton yang belum dilunakkan pada tegangan puncak selama uji silinder
ε1 , ε2
regangan tarik beton (positif), regangan tekan beton (negatif)
adalah d , ε r
rata-rata regangan utama dalam arah d dan r
itu ds
regangan maksimum pada permukaan beton
aku , aku t
rata-rata regangan normal dalam arah l dan t
ε ly , ε ty
regangan luluh baja pada arah l dan t
aku
koefisien pelunakan beton
θ
kemiringan tegangan utama terhadap sumbu x
θ c
sudut penyangga kompresi
θ cr
sudut retakan yang diamati dalam pengujian
θ c ,lebih rendah
batas bawah sudut penyangga
θ c ,atas
batas atas sudut penyangga
θ ε
sudut kemiringan regangan utama terhadap sumbu x
atau f
fraksi volume serat
jika l , t ( ρ x , ρ y )
rasio baja pada arah l dan t
saya l , saya t
diameter batang baja longitudinal dan transversal
saya c l , saya c t
tegangan normal rata-rata beton dalam arah l dan t
kita d , kita r
tegangan utama dalam arah d dan r
saya l , saya t
tegangan normal rata-rata beton pada arah l dan t
kita 1 , kita 2
tekanan yang diterapkan dalam 1–2 arah
saya b
tegangan ikatan antara serat dan beton
dari
tegangan geser rata-rata dalam koordinat lt
