Abstrak
Memprediksi perkembangan proses retak pada elemen struktural yang terbuat dari beton bertulang (RC) atau komposit semen lainnya masih merupakan tugas yang menantang. Meskipun prosedur eksperimental yang mapan diadopsi secara luas dengan tujuan untuk mendapatkan pengetahuan empiris tentang proses yang disebutkan di atas, belum ada konsensus serupa yang dicapai tentang pemodelan mekanis. Sebenarnya, pendekatan simulasi yang tersedia dalam literatur didasarkan pada model elemen hingga 3D yang menuntut komputasi atau pada solusi 1D yang disederhanakan yang diperoleh melalui strategi numerik alternatif, seperti skema perbedaan hingga. Makalah ini mengusulkan model FEM yang disederhanakan berdasarkan elemen pegas 1D, yang bertujuan untuk memperoleh keseimbangan yang wajar antara akurasi simulasi dan upaya komputasi. Skema iteratif-inkremental yang mendorong prosedur solusi nonlinier dijelaskan secara rinci dan beberapa perbandingan dengan hasil eksperimen pada anggota tarik RC diusulkan dengan tujuan memvalidasi model yang diusulkan. Selain itu, hasil yang menjanjikan yang diperoleh dalam makalah ini menginspirasi pengembangan penelitian di masa mendatang menuju simulasi numerik perilaku retak komposit matriks anorganik lainnya, seperti mortar bertulang tekstil (TRM), yang mengalami tindakan tarik.
1. PENDAHULUAN
Pembentukan retak pada komponen beton bertulang (RC) merupakan masalah yang relevan karena sifat getas komposit semen ini di bawah beban tarik. 1 Oleh karena itu, batang tulangan ditanamkan dalam beton dengan tujuan untuk mengendalikan pembentukan retak dan mewujudkan daya dukung yang cukup pada komponen RC. Namun, ketika beban tarik mencapai ketahanan matriks beton, ikatan antara batang tulangan dan matriks beton memainkan peran penting dalam pembentukan retak, karena mengendalikan perpindahan tegangan antara beton retak dan tulangan yang tertanam.
Uji tarik merupakan prosedur rekayasa yang berguna untuk menentukan beberapa karakteristik penting dari anggota yang mengalami tarikan yang terbuat dari material atau komposit tertentu. 2 Tujuan dari pengujian ini adalah untuk menyimpulkan kurva tegangan-regangan (atau gaya-perpindahan) dan hubungan ikatan-selip. Kedua elemen ini merupakan informasi terpenting untuk menentukan perilaku anggota RC yang mengalami tarikan. 3
Beberapa model telah diformulasikan dalam literatur dengan tujuan untuk memahami fenomena retak beton dan memprediksi efeknya pada respons tarik anggota RC. 4 , 5 Lebih khusus lagi, model numerik yang tersedia dalam literatur umumnya didasarkan pada Metode Elemen Hingga (FEM), meskipun dengan berbagai tingkat detail dan biaya komputasi. 6 – 8 Beberapa di antaranya diimplementasikan melalui kode elemen hingga 3D. 9 – 11 Pendekatan pemodelan lainnya didasarkan pada prosedur numerik lain yang menuntut komputasi. 12 – 16 Pada prinsipnya, analisis FEM dapat memprediksi beberapa fitur fenomena retak beton, seperti resistensi mekanis, inisiasi dan perambatan retak, perilaku interaksi tulangan-matriks. 17
Di sisi lain, model yang lebih sederhana yang tersedia dalam literatur didasarkan pada penggunaan skema perbedaan hingga (FD) untuk menyelesaikan persamaan keseimbangan dan kompatibilitas 1D yang mengendalikan perilaku anggota RC yang mengalami beban tarik. 18
Model saat ini terdiri dari prosedur nonlinier sederhana yang didasarkan pada perakitan elemen seperti pegas/batang. Oleh karena itu, model ini menggabungkan konsistensi matematis FEM dengan kesederhanaan formulasi 1D, seperti dalam kasus solusi FD yang disebutkan sebelumnya. Meskipun model saat ini ditujukan untuk mensimulasikan perilaku retak anggota beton RC yang dikenai beban tarik, pada prinsipnya, model ini dapat digunakan untuk mensimulasikan perilaku tarik sistem struktural serupa lainnya (misalnya komposit Mortar Bertulang Tekstil).
Sebenarnya, model saat ini didasarkan pada prosedur numerik yang cukup baru berdasarkan asumsi mekanis yang disederhanakan, meskipun mempertimbangkan semua sifat relevan yang memengaruhi fenomena retak, termasuk kekuatan tarik beton dan interaksi ikatan antara matriks beton dan tulangan baja.
Oleh karena itu, model yang diusulkan didasarkan pada beberapa asumsi untuk mereproduksi fenomena fisik, dengan mempertimbangkan parameter utama yang mengatur fenomena tersebut. Lebih khusus lagi, model ini didasarkan pada skema geometri 1D dengan asumsi skala observasi makroskopis yang sedang diselidiki. Asumsi yang disederhanakan ini menghasilkan model yang sangat efisien secara komputasi yang dapat dengan mudah dikodekan dalam Matlab (atau bahasa serupa) dan dapat dijalankan pada laptop biasa dalam beberapa menit.
Perlu digarisbawahi bahwa model saat ini menempatkan dirinya dalam posisi perantara antara model “resolusi rendah” dan “resolusi tinggi”. 19 Di satu sisi, ia mengasumsikan deskripsi geometris yang disederhanakan, seperti dalam masalah resolusi rendah. Di sisi lain, ia secara eksplisit mensimulasikan diskontinuitas perpindahan (misalnya, terjadinya slip relatif) antara perpindahan beton dan baja di seluruh antarmuka mereka. Makalah saat ini terstruktur sebagai berikut: Bagian 2 merumuskan model dengan menyajikan berbagai elemen pegas yang terdiri dari model dan menguraikan perakitannya; Bagian 3 merangkum prosedur solusi inkremental-iteratif nonlinier. Bagian 4 menyajikan hasil dan validasi model yang diusulkan; Akhirnya, Bagian 5 menyoroti kesimpulan utama dan gambar menguraikan perkembangan masa depan dari penelitian saat ini.
2 PERUMUSAN MODEL PEGAS UNTUK ANGGOTA RC YANG TERKENA TEGANGAN
Model yang diusulkan dikembangkan dengan tujuan untuk mensimulasikan respons mekanis batang tulangan yang tertanam di dalam matriks beton yang dipasang pada salah satu dari dua ujung dan dikenakan beban tarik yang diberikan pada ujung lainnya. Dua “fase” dari sistem “komposit” ini dimodelkan oleh dua orde elemen pegas, satu untuk matriks beton dan yang lainnya untuk batang tulangan. Model ini didasarkan pada perakitan elemen seperti pegas 1D yang dimaksudkan untuk mensimulasikan perilaku anggota RC yang dikenakan beban tarik: Gambar 1 menunjukkan representasi skematis dari anggota tarik RC yang dipertimbangkan.

2.1 Perumusan elemen pegas
Model ini mengasumsikan idealisasi yang digambarkan pada Gambar 2 di mana berbagai elemen pegas/batang disorot:
- beton tidak retak;
- batang penguat;
- ikatan baja–beton;
- antarmuka panjang nol yang mewakili kemungkinan retakan beton;
- antarmuka panjang nol yang mewakili sambungan antara dua pegas batang penguat yang berdekatan.
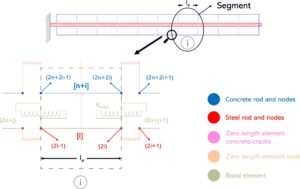
Model numerik uji tarik dengan elemen rangka 1D.
Elemen RC yang diberi tegangan diskemakan menjadi n segmen (Gambar 1 ). Setiap segmen RC dimodelkan oleh dua elemen pegas/batang yang dimaksudkan untuk mensimulasikan hubungan antara gaya aksial dan perpindahan yang diterapkan pada dua simpul yang sesuai. Lebih khusus lagi, pada segmen RC ke -i , dua pegas yang disebutkan di atas diberi nomor sebagai [ i ] (tulang baja) dan [ n + i ] (beton yang sesuai).
Interaksi ikatan antara beton dan tulangan disimulasikan oleh elemen pegas dua simpul lebih lanjut yang menghubungkan simpul-simpul yang sesuai dari dua pegas yang disebutkan sebelumnya (Gambar 2 ).
Pegas beton dan tulangan baja yang berdekatan pada setiap segmen RC dihubungkan satu sama lain dengan menggunakan elemen pegas “panjang nol” lainnya yang, dalam rentang elastis respons struktural, menghadirkan kekakuan aksial yang secara nominal tak terbatas.
2.1.1 Batang tulangan
Batang merah pada Gambar 2 merupakan batang tulangan dari elemen ke -i dan dilambangkan dengan indeks [ i ], di mana i adalah indeks setiap segmen. Matriks kekakuan elemen ini dapat didefinisikan dengan mudah sebagai berikut:







3 PROSEDUR SOLUSI NONLINIER
3.1 Masalah Nonlinier
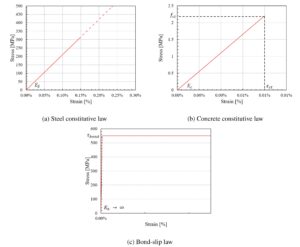
Bagian 2 menguraikan formulasi model dalam rentang elastis linier. Namun, fenomena retak yang dipertimbangkan dikendalikan oleh perilaku material nonlinier. Lebih khusus lagi, model tersebut berfokus pada perilaku retak beton dalam tarikan dan juga mempertimbangkan perilaku kaku-plastik untuk hukum ikatan baja-beton.
Prosedur nonlinier yang dirinci di bawah ini didasarkan pada prosedur iteratif-inkremental yang umum.
3.1.1 Analisis retak
Uji tarik terutama ditujukan untuk mengamati urutan acak pembentukan dan perambatan retak beton. Pembentukan retak terutama dikontrol oleh:
- Retakan beton;
- Hukum ikatan-slip antarmuka.
Aspek pertama terkait dengan kekuatan tarik matriks. Dengan tujuan untuk mempertimbangkan kekuatan tarik beton yang cukup bervariasi di seluruh anggota beton (yang diperlukan untuk memperkenalkan variabilitas alami dalam model numerik), nilai kekuatan tarik berikut diberikan pada elemen pegas panjang nol beton generik 18 :

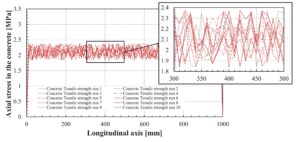
Pola pembentukan retakan digambarkan pada Gambar 5 : pola ini menunjukkan evolusi tegangan aksial dalam beton. Pembentukan retakan pada segmen tertentu menyebabkan putusnya pegas beton tersebut (lihat Gambar 2 ) dan, akibatnya, tidak ada tegangan pada titik lokal tersebut.
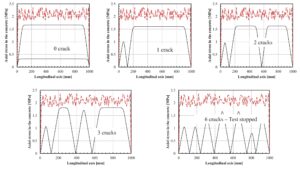
Aspek lain yang relevan terkait dengan kapasitas elemen penguat untuk mengembangkan tegangan ikatan antarmuka. Kedua aspek tersebut dirinci dan dibahas dalam subbagian berikut.
3.2 Prosedur numerik iteratif-inkremental
Model elastis linier yang diformulasikan dalam Bagian 2 dapat dimasukkan dalam prosedur iteratif-bertahap yang dimaksudkan untuk mensimulasikan perkembangan progresif fenomena retak. Lebih khusus lagi, solusi linier yang disebutkan di atas memainkan peran sebagai “prediktor elastis” yang diikuti oleh “korektor” nonlinier 6 yang dimaksudkan untuk memperkenalkan interaksi ikatan nonlinier dan kemungkinan pembentukan retak di mana tegangan tarik dalam beton mencapai kekuatan tarik yang sesuai.
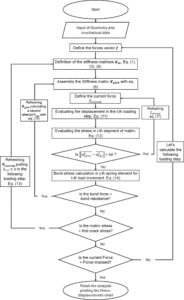
Gambar 6 menunjukkan diagram alir dari prosedur nonlinier yang diterapkan dalam karya ini. Perlu dijelaskan bagaimana model mencapai solusi melalui matriks dan vektor yang didefinisikan dalam paragraf sebelumnya. Subbagian berikut melaporkan rincian lebih lanjut tentang urutan prediktor-korektor sebagai bagian dari prosedur iteratif-bertahap, yang pengodeannya saat ini dikembangkan sepenuhnya di Matlab. 20 Subbagian berikut menunjukkan bagaimana model menemukan solusi menggunakan matriks dan vektor dari paragraf terakhir. Subbagian tersebut juga memberikan rincian lebih lanjut tentang proses prediktor-korektor, yang merupakan bagian dari prosedur iteratif-bertahap.


4 UJI MODEL DAN VALIDASI MODEL
4.1 Uji Numerik
Bagian ini mengusulkan hasil analisis numerik yang dijalankan pada elemen tarik RC umum (TM) yang terdiri dari prisma beton yang di ujungnya diberi beban tarik (Gambar 1 ). Tabel 1 melaporkan geometri utama dan parameter mekanis yang dipertimbangkan dalam analisis awal, yang dilakukan dalam kontrol perpindahan.
| Parameter | Simbol | Nilai | Satuan |
|---|---|---|---|
| Panjang total sampel | Ltot | 1000 | satuan |
| Jumlah elemen | nEl | 100 | – |
| Koefisien | μ | 1.5 | – |
| Modulus Young Baja | Es | 210.0 | IPK |
| Modulus Young Beton | Ec | 27.5 | IPK |
| Diameter batang | ds | 20 | satuan |
| Lebar penampang beton | bc | 100 | satuan |
| Kedalaman penampang beton | hc | 100 | satuan |
| Kekakuan antarmuka | kb | 1×104 | MPa |
| Kekakuan sambungan beton | kc | 1×109 | MPa |
| Kekuatan tarik karakteristik beton | fct | 2.16 | MPa |
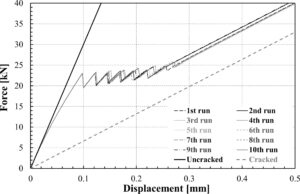
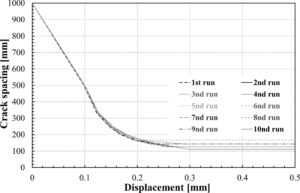
Gambar 7 menunjukkan tren khusus dari uji tarik yang dilakukan pada beton bertulang. Secara umum, ada tiga bagian: bagian linier pertama, bagian kedua yang disebut “zona retak” dan bagian terakhir hingga sampel pecah. Gambar 8 menunjukkan kurva jarak retak yang terkait dengan kurva yang dilaporkan pada Gambar 7 .
4.2 Pengaruh variabilitas aleatorik terhadap kekuatan beton
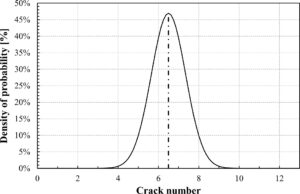
Variabilitas kekuatan beton, dijelaskan oleh ( 10 ), menyebabkan variabilitas dalam hasil numerik. Sepuluh kali pengujian dilakukan pada model dengan data Tabel 1 dan diperoleh hasil yang sedikit berbeda. Gambar 9 menunjukkan kerapatan probabilitas jumlah retak untuk 10 kali pengujian pada model. Nilai rata-rata yang sama dengan 6,5 retak ditemukan dalam seri 10 kali pengujian dan jumlah retak berkisar antara 5 dan 8. Perbedaan jumlah retak menghasilkan CoV sebesar 13%, nilai rendah ini menunjukkan stabilitas dan keandalan yang sangat baik dari hasil numerik, yang menunjukkan bahwa hasilnya konsisten dan tidak dipengaruhi secara signifikan oleh variasi acak, meskipun variabilitas acak juga diperhitungkan oleh model. Perbedaan ini terkait dengan nilai acak dalam ( 10 ) yang mewakili variabilitas alami beton.
Selain itu, Gambar 8 menunjukkan perbandingan antara kurva jarak retak dari 10 pengujian, yang kurva gaya-perpindahannya dilaporkan pada Gambar 7. Kurva-kurva ini serupa dengan sedikit perbedaan di zona terakhir, di mana jumlah retak yang sedikit bervariasi diperoleh.
4.3 Wawasan lebih lanjut tentang simulasi numerik
Penggunaan simulasi numerik sebagai pengganti uji eksperimental memberikan keuntungan untuk menemukan wawasan lebih jauh. Beberapa wawasan berguna untuk lebih memahami sifat mekanis matriks dan penguat.
Gambar 10a menunjukkan dua kurva penting: tegangan aksial yang terbentuk pada beton dan distribusi stokastik kekuatan retak pertama pada sampel. Kurva putus-putus mengasumsikan nilai nol pada simpul tempat retakan terbentuk. Awalnya, nilai kurva putus-putus meningkat secara monoton hingga memotong kurva kontinu. Setelah perpotongan terjadi, tegangan aksial yang terkait dengan absis perpotongan adalah nol.

Gambar 10b menunjukkan slip antara dua fase sampel pada panjang bebas dan tegangan ikatan yang terbentuk. Grafik tersebut menggambarkan perpindahan timbal balik antara mortar dan batang baja: tujuh lompatan pada grafik menunjukkan tujuh zona pada sampel tempat retakan terjadi.
Gambar 10c menunjukkan tegangan ikatan antara dua fasa batang RC. Nilai tegangan ikatan dibatasi oleh nilai gaya resistansi ikatan. Mirip dengan dua gambar sebelumnya, kurva menunjukkan adanya tujuh retakan.
Lebih jauh lagi, tiga gambar yang sejajar secara vertikal menekankan hubungan timbal balik dari sifat-sifat mekanik yang direpresentasikan pada sumbu-y: peningkatan slip antarmuka menyebabkan peningkatan tegangan ikatan, dan keduanya bergantung pada tegangan aksial pada beton dan kekuatan aksialnya.
4.4 Pengaruh diskritisasi model
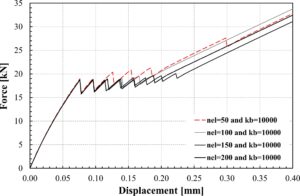
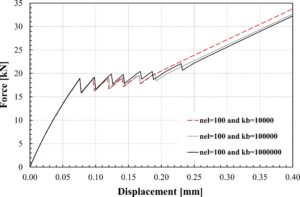
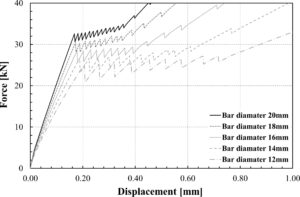
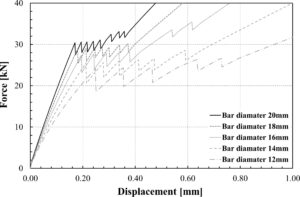
Sangat menarik untuk mengevaluasi pengaruh dua parameter diskritisasi numerik yang memengaruhi respons kurva gaya-perpindahan. Parameter yang memainkan peran ini adalah jumlah elemen dan kekakuan antarmuka. Gambar 11 menunjukkan kurva yang diperoleh dari empat analisis yang dijalankan pada model yang terdiri dari sejumlah elemen mulai dari 50 hingga 200. Hal ini menunjukkan bahwa analisis tersebut tidak menghasilkan hasil yang tampak berbeda.



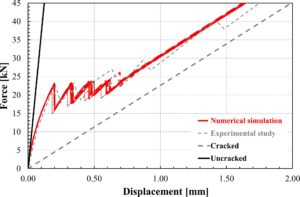
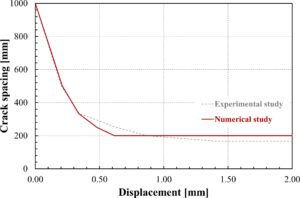

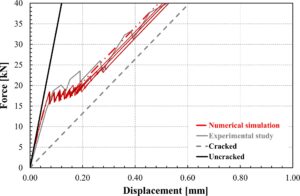
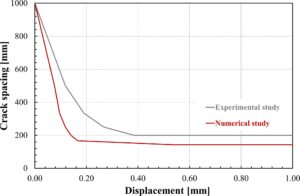
Gambar 18 menunjukkan perbandingan jarak retak antara hasil eksperimen dan hasil numerik.

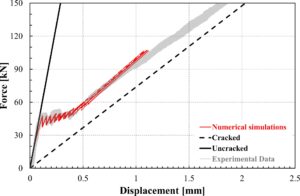
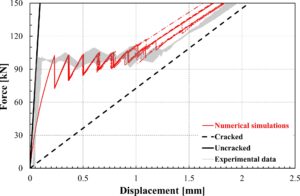

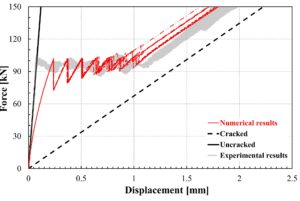
Model yang dikembangkan dalam studi ini didasarkan pada formulasi standar metode elemen hingga, meskipun hanya menggunakan elemen pegas/batang sederhana yang dimaksudkan untuk mensimulasikan material yang mengalami tegangan, interaksi ikatan antara beton dan tulangan, dan elemen dengan panjang nol yang menghubungkan elemen beton dan tulangan yang berdekatan. Model yang diusulkan dimaksudkan untuk menentukan evolusi tegangan dan regangan di seluruh anggota RC tarik dan mensimulasikan pembentukan retakan secara progresif.
Perbandingan yang diusulkan dengan hasil eksperimen yang tersedia dalam literatur menegaskan bahwa model yang diusulkan sebenarnya mampu mereproduksi pengamatan eksperimen dengan biaya komputasi yang cukup terbatas. Lebih khusus lagi:
- analisis yang diajukan secara umum menghasilkan kurva gaya–perpindahan yang cukup akurat;
- di samping kemungkinan adanya perbedaan, model tersebut terbukti mampu memperkirakan jumlah retakan dan, dengan demikian, jarak retakan rata-rata di antara retakan tersebut, yang merupakan salah satu parameter mekanis utama yang mencirikan anggota RC dalam tegangan;
- pengaruh distribusi aleatorik kekuatan tarik beton di seluruh panjang anggota beton dapat dengan mudah dimasukkan dalam analisis numerik yang diusulkan.
Akhirnya, perlu digarisbawahi bahwa model saat ini, meskipun divalidasi di sini untuk mensimulasikan perilaku anggota RC dalam ketegangan, idealnya dapat diadaptasi dan diperluas dengan tujuan untuk menganalisis respons tarik dari sistem mekanis dan bahan serupa lainnya, seperti beton bertulang serat atau komposit mortar bertulang tekstil.
