Abstrak
Studi ini menjelaskan penilaian ketahanan struktur beton bertulang 3D dengan menganalisis respons rangka 2D dalam konfigurasi desain dan skenario kegagalan yang berbeda. Struktur dicirikan oleh rangka dengan balok lebar dan rangka tahan gempa dengan balok dalam. Tiga konfigurasi desain struktural diselidiki: konfigurasi kode dan dua konfigurasi yang ditingkatkan berkenaan dengan ketahanan. Untuk konfigurasi apa pun, empat skenario kegagalan yang berbeda dipertimbangkan, dengan menghilangkan kolom pendukung tertentu. Untuk skenario kegagalan dan konfigurasi desain apa pun, simulasi elemen hingga non-linier (NLFE) 2D dilakukan untuk mengevaluasi perilaku dua rangka di sepanjang dua arah ortogonal. Dalam analisis apa pun, kontribusi rangka, yang terletak di sepanjang arah ortogonal, dipertimbangkan melalui pegas translasi yang memiliki hukum konstitutif non-linier yang khusus untuk gerakan ke dalam dan ke luar. Dengan memaksakan perpindahan yang meningkat di bagian atas kolom yang dihilangkan, kurva kapasitas yang sesuai telah ditetapkan. Secara berurutan, dua kurva kapasitas NLFE bidang ditumpangkan untuk menentukan respons global dari struktur rangka. Superposisi ini divalidasi melalui perbandingan dengan analisis non-linier 3D. Hasilnya menunjukkan pentingnya mengkalibrasi hukum konstitutif non-linier pegas, khususnya untuk perpindahan vertikal besar dan beberapa skenario kegagalan. Rangka dengan balok lebar meningkatkan, khususnya, duktilitas global. Selain itu, superposisi kurva kapasitas NLFE bidang dari dua rangka ortogonal dikonfirmasi. Akhirnya, melalui pendekatan berbasis energi, manfaat dari peningkatan desain ketahanan disorot.
1. PENDAHULUAN
Saat ini, komunitas ilmiah menghadapi kebutuhan untuk memperhitungkan skenario desain yang tidak dipertimbangkan di masa lalu, seperti peristiwa ekstrem. Peristiwa ekstrem adalah situasi yang sangat tidak mungkin terjadi tetapi memiliki konsekuensi bencana dalam hal kerugian ekonomi, kematian, dan cedera. 1 Kekokohan struktural adalah konsep utama karena mewakili respons yang harus diberikan sistem saat terjadi peristiwa ekstrem atau, dengan kata lain, untuk menghindari fenomena keruntuhan yang tidak proporsional atau progresif. 2 Salah satu metode yang paling luas untuk mengevaluasi kekokohan struktural bangunan beton bertulang (RC) adalah mempelajari jalur beban alternatif (yaitu, analisis ALP) dengan melepas kolom pendukung, seperti yang disarankan oleh kode dan pedoman. 3 – 7 Mekanisme membran (dalam kasus elemen pelat penuh) atau katenari (dalam kasus elemen balok) merupakan aspek penting untuk diselidiki karena keduanya menjamin tingkat daya dukung tertentu jika kolom pendukung dilepas. Misalnya, dalam Droogné et al. 8 keandalan rangka RC planar di bawah skenario kehilangan kolom dipelajari, dengan memperhitungkan, dengan cara yang disederhanakan, aksi membran yang berkembang antara elemen yang terpengaruh secara langsung dan tidak langsung. Validasi numerik pada tiga sub-rakitan balok-kolom-pelat RC skala nyata dikembangkan di Botte et al. 9 untuk mempelajari parameter yang memengaruhi aktivasi aksi membran tarik (yaitu, kondisi kendala, ketebalan pelat, rasio tulangan). Penilaian keruntuhan seismik dan progresif pada struktur rangka RC dilakukan di, 10 untuk menyelidiki efektivitas intervensi retrofit. Studi eksperimental pada strip pelat RC di bawah beban geser dan tarik dipelajari secara numerik di Belletti et al., 11 untuk menilai peningkatan kekokohan struktural karena aktivasi efek membran. Faktanya, retakan yang dihasilkan pada ekstrados lantai RC kontinu yang dekat dengan kolom yang hilang secara tidak sengaja menghasilkan kondisi kendala pada ekspansi radial dan, dengan demikian, gaya membran yang meningkatkan kapasitas menahan beban sistem. 12 – 15 Namun, sebagian besar hasil ini mempertimbangkan pelat penuh yang memiliki ketebalan lebih dari 15–20 cm. Tiga dimensi ini tidak hanya dijamin oleh pelat tetapi juga oleh rangka dalam arah ortogonal. 16 Misalnya, pentingnya memasukkan rangka melintang dalam model skenario keruntuhan progresif ditunjukkan oleh perbandingan numerik antara analisis 2D dan 3D dalam Fascetti et al., 17 Brunesi dan Parisi. 18Kesimpulan ini juga dicapai melalui analisis eksperimental pada ketahanan keruntuhan progresif dari subrakitan balok-kolom yang mempertimbangkan efek balok melintang. 19 Secara khusus, ditunjukkan bahwa kurva kapasitas untuk subrakitan balok melintang hampir bertepatan dengan superposisi balok memanjang dan balok melintang. Sebuah studi eksperimental dan numerik tentang keruntuhan progresif untuk struktur RC tiga dimensi dilakukan di Guo et al. 20 yang mengusulkan model analitis untuk menyertakan efek balok sekunder dan torsi balok primer. Hasil eksperimen di Qian et al. 21 menunjukkan bahwa efek 3D, tidak termasuk pelat, dapat meningkatkan daya dukung rangka lebih dari 100%. Kesimpulan serupa ditarik oleh Li H dan El-Tawil 22 dengan perbandingan numerik antara sistem planar dan model 3D. Masalah ini dapat sangat relevan untuk bangunan yang memiliki pelat dengan balok satu arah (umum, misalnya, di Italia). Namun, analisis 3D, terutama di bidang dinamis, tidak selalu menjadi pilihan yang lebih baik karena memerlukan upaya komputasi dan keahlian yang besar.
Adapun, khususnya, struktur yang memiliki pelat dengan balok satu arah, studi ini mengusulkan untuk menyertakan beberapa efek tiga dimensi yang relevan dengan menyelidiki kapasitas dukung dari dua rangka planar ortogonal yang secara langsung terlibat dalam skenario pelepasan kolom. Oleh karena itu, analisis parametrik yang besar dilakukan untuk menilai kekokohan struktur penahan momen (MR) RC biasa 3D yang menganalisis respons rangka planar sepanjang dua arah ortogonal. Struktur 3D terletak di zona seismik tinggi dan dicirikan oleh rangka dengan balok lebar dan rangka tahan seismik dengan balok dalam, yang dirancang menurut kode Italia 23 dan Eropa 24. Secara khusus, terinspirasi oleh Miceli dan Castaldo, 25 Miceli et al. 26 tiga struktur yang sesuai dengan tiga konfigurasi desain diselidiki: yang STANDARD menurut kode dibandingkan dengan konfigurasi yang memiliki tulangan longitudinal balok yang kontinu, simetris, dan sama di semua lantai sebagai tambahan pada tulangan sisi muka (dilambangkan sebagai CSE + tulangan ) dan, kemudian, dengan konfigurasi di mana simetri dan kesetaraan lantai dikecualikan (dilambangkan sebagai C + tulangan ). Untuk ketiga konfigurasi desain, empat skenario kegagalan yang berbeda dipertimbangkan dengan membuang kolom pendukung tertentu. Untuk setiap skenario kegagalan dan konfigurasi desain tertentu, simulasi dorong ke bawah elemen hingga non-linier (NLFE) 2D dilakukan untuk mengevaluasi perilaku dua rangka RC sepanjang dua arah ortogonal. Dalam setiap simulasi 2D, kontribusi rangka ortogonal diperhitungkan melalui pegas translasi yang memiliki hukum konstitutif non-linier yang dikalibrasi dengan tepat sepanjang arah ke dalam dan ke luar. Dengan memaksakan perpindahan yang meningkat di bagian atas kolom yang dibuang, kurva kapasitas yang sesuai didefinisikan. Secara berurutan, kurva kapasitas NLFE bidang ini ditumpangkan untuk memperoleh respons global struktur. Superposisi ini divalidasi melalui perbandingan dengan kurva kapasitas non-linier 3D yang sesuai. Hasilnya menunjukkan pentingnya mengkalibrasi hukum konstitutif non-linier pegas, khususnya untuk perpindahan vertikal yang besar dan beberapa skenario kegagalan ketika bangunan juga memiliki balok yang lebar. Faktanya, rangka dengan balok yang lebar memberikan kontribusi, khususnya dalam hal duktilitas. Selain itu, hasilnya memvalidasi superposisi kurva kapasitas NLFE bidang dari dua rangka ortogonal, yang terlibat dalam skenario kegagalan yang sama, untuk menentukan kurva kapasitas global untuk konfigurasi desain dan skenario kegagalan yang berbeda. Akhirnya, pendekatan kesetaraan energik 27memungkinkan penilaian efektivitas perbaikan desain pada rangka bidang untuk meningkatkan kekokohan struktur 3D terhadap berbagai skenario kegagalan.
2 KEKUATAN STRUKTUR RC: ANALISIS DAN USULAN
Perilaku struktural rangka beton bertulang dalam kasus skenario kehilangan kolom telah dipelajari secara luas melalui uji eksperimental pada subrakitan balok-kolom. 28 – 31 Respon ini, yang dinyatakan dalam kurva kapasitas (yaitu, kurva beban-perpindahan), menyajikan tiga fase: (i) fase pertama (yaitu, fase lengkung-lentur ) yang diatur oleh pembengkokan balok dengan perpindahan horizontal luar dari simpul balok-kolom yang disebabkan oleh gaya aksial tekan pada balok; fase ini berakhir ketika puncak resistansi tercapai, yang dilambangkan di sini sebagai
; (ii) fase kedua (yaitu, fase pelunakan ) di mana respons pelunakan terjadi dengan pengurangan perpindahan horizontal dan reaksi di titik pelepasan kolom akibat penghancuran beton; (iii) fase ketiga (yaitu, efek katenari ) yang memiliki peningkatan reaksi untuk perpindahan vertikal yang lebih tinggi di titik pelepasan dengan perpindahan horizontal ke dalam dari simpul balok-kolom; fase ini berakhir dengan keruntuhan atau puncak pamungkas, yang diidentifikasi sebagai P MAX,ULT , dan diatur oleh respons tulangan longitudinal.
Perhatikan bahwa pengaruh yang relevan dari gaya kompresi aksial pada balok dapat terjadi terutama pada fase pertama dan juga pada fase kedua.
Menurut pendekatan energetik oleh Izzuddin et al. 27 kurva kapasitas berguna untuk menentukan kerja internal U i (yaitu, energi yang diserap oleh struktur ketika kolom dilepas), sedangkan kerja eksternal W ext (yaitu, kerja yang dilakukan oleh beban gravitasi) disediakan oleh reaksi P EXT yang sesuai dari kolom sebelum dilepas. Reaksi ini dihitung dalam kombinasi aksidental beban eksternal (yaitu, beban struktural permanen, beban non-struktural, dan beban variabel) sesuai dengan kode. 23 , 24 Titik kinerja (yaitu, titik keseimbangan dinamis) kemudian dievaluasi dalam korespondensi kesetaraan antara kerja eksternal dan energi internal.
Mengenai kerangka sistem RC, berbagai studi literatur dan kode telah memberikan ketentuan berikut untuk meningkatkan perilaku ketahanan:
- Simetri ( S ): rekomendasi yang diberikan oleh kode dan studi literatur (misalnya, 7 , 32 ) terdiri dari pengaturan tulangan yang sama di dua tali balok, menjadikan penampang simetris;
- Dukungan-kontinuitas : jika batang tulangan longitudinal kontinu di atas dukungan, mereka berguna untuk mendukung perilaku ikatan balok 4 – 6 , 33 – 35 ;
- Pegas elastis lateral ekuivalen : keberadaan sistem struktur ortogonal dapat sangat dan positif mempengaruhi respon struktur ketika kolom pendukung runtuh, seperti yang ditunjukkan dalam Referensi [ 12 , 16 – 19 , 36 ]. Seperti yang diamati dalam Miceli dan Castaldo, 25 penerapan pegas elastis horizontal ekuivalen mempengaruhi secara signifikan aktivasi perilaku katenari;
- Kesetaraan lantai ( E ): disarankan untuk menerapkan jumlah tulangan yang sama pada semua lantai seperti pada lantai pertama (yaitu yang terbesar) untuk mencapai perilaku Vierendeel 25 ;
- Kontinuitas ( C ): sangat penting untuk memiliki batang tulangan longitudinal yang kontinu di atas tumpuan dan sepanjang balok (yaitu, tidak kurang dari 30% dari panjang bentang) di samping panjang jangkar di setiap tepi balok, terutama di tali busur atas balok, seperti yang diusulkan dalam Miceli dan Castaldo 25 ;
- Tulangan sisi muka : tulangan sisi muka menentukan peningkatan penting. Bahkan, seperti yang diusulkan dalam Miceli dan Castaldo, 25 tulangan ini penting untuk mengantisipasi transisi menuju aktivasi katenari pada perpindahan vertikal yang lebih rendah dari kedalaman penampang balok.
Modifikasi tulangan longitudinal ini mempengaruhi desain seismik berkenaan dengan prinsip desain kapasitas dan perancangan ulang siklus batas ultimit dan batas kemampuan layanan (U-SLS) serta verifikasi seismik, oleh karena itu, diperlukan, seperti yang dibahas dalam Miceli dan Castaldo. 25
Dalam kajian ini, isu-isu tambahan berikut ini, yang berguna bagi desain dan analisis berkenaan dengan respons ketahanan, diselidiki:
- Pegas lateral non-linier : hukum konstitutif pegas dikalibrasi dengan tepat untuk gerakan ke dalam dan ke luar guna memodelkan kontribusi horizontal yang diberikan oleh sistem ortogonal di luar bidang (yaitu, balok dan kolom rangka ortogonal di luar bidang). Dengan cara ini, seluruh perkembangan respons mekanis semua rangka diperhitungkan secara eksplisit mulai dari perilaku elastis penuh hingga perilaku tidak elastis penuh semua balok dan kolom;
- Superposisi kurva kapasitas 2D : untuk kehilangan kolom tertentu, respons nonlinier bidang dari dua rangka ortogonal yang secara langsung dipengaruhi oleh skenario kegagalan yang sama dihitung dan kemudian ditumpangkan untuk memperoleh kurva kapasitas global termasuk efek nonlinier 3D yang sesuai di sepanjang dua arah. Validasi superposisi ini dilakukan melalui perbandingan dengan kurva kapasitas yang sesuai yang diperoleh dari analisis nonlinier 3D.
Proposal-proposal ini diuji dengan menggunakan analisis parametrik yang luas: tiga struktur RC MR biasa 3D, yang memiliki pelat dengan balok satu arah dan terdiri dari balok lebar dan dalam, yang sesuai dengan tiga konfigurasi desain yang berbeda diperiksa sehubungan dengan empat skenario kegagalan. Secara rinci, konfigurasi desain kode STANDARD dibandingkan dengan konfigurasi struktural yang memiliki semua rekomendasi sebelumnya (yaitu, CSE + tulangan ) dan kemudian dengan konfigurasi desain tanpa simetri dan kesetaraan lantai (yaitu, C + tulangan ). Berikut ini, tiga konfigurasi desain dianalisis dengan menggunakan model NLFE 2D untuk empat skenario kegagalan yang menarik bagi masalah ketahanan.
3 KONFIGURASI DESAIN YANG BERBEDA UNTUK STRUKTUR 3D DI ZONA SEISMIK
Bagian ini membahas desain tiga struktur 3D yang sesuai dengan tiga konfigurasi desain untuk menguji proposal.
Konfigurasi struktural pertama yang dilambangkan sebagai desain STANDARD mengacu pada bangunan biasa 3D, yang terdiri dari rangka RC MR bertingkat, dengan tinggi antar lantai 3,5 m, elevasi teratur dan simetris di kedua arah. Denah bangunan, diilustrasikan dalam Gambar 1 , memiliki empat bentang di arah x dan tiga di arah y dengan panjang bentang 5 m di kedua arah. Selain itu, garis putus-putus pada Gambar 1 menunjukkan balok lebar yang sejajar dengan arah balok pelat satu arah, sedangkan garis kontinu menunjukkan balok dalam. Dalam karya ini, balok lebar menunjukkan balok yang memiliki kedalaman yang sama dengan pelat termasuk balok, sedangkan balok dalam lebih tinggi dari tinggi pelat dan balok. Oleh karena itu, sistem RC memiliki rangka 2D dengan geometri dan karakteristik ketahanan yang berbeda untuk mewakili studi kasus generik. Lebih jauh, Gambar 1 menunjukkan skenario kegagalan yang dipelajari yang mewakili kemungkinan kerusakan lokal yang dapat memicu keruntuhan progresif.
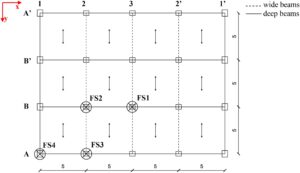
Desain STANDARD dilakukan dengan menggabungkan beban gravitasi dengan aksi salju dan angin menurut Referensi [ 3 , 23 ] serta mengikuti pedoman desain seismik dari NTC2018 23 dan EC8, 24 dengan mengasumsikan kota L’Aquila (Italia) sebagai lokasi referensi dan kelas daktilitas tinggi. Penting untuk digarisbawahi bahwa balok dalam termasuk rangka tahan seismik, sementara rangka lain dengan balok lebar dirancang sebagai elemen struktural sekunder menurut Referensi [ 23 , 24 ]. Ketinggian balok yang besar pada rangka MR telah dipilih untuk meningkatkan kapasitas dukung rangka sesuai dengan. 30 Pada saat yang sama, rasio tinggi-lebar yang relatif besar (yaitu, 80%) dapat bermanfaat untuk meningkatkan respons lengkung-lentur serta memfasilitasi perilaku yang lebih daktail untuk katenari. 37 Pada semua elemen struktur, beton C25/30 23 digunakan, dengan menggunakan selimut beton bening 3,5 cm. Untuk tulangan longitudinal dan transversal, batang baja B450C 23 digunakan sebagai berikut: ϕ18 untuk tulangan longitudinal balok dalam, ϕ14 untuk tulangan longitudinal balok lebar, ϕ20 untuk kolom dan ϕ8 untuk sengkang. Pada semua simpul balok-kolom, sengkang ϕ8 ditempatkan dengan jarak 50 mm. Jarak sengkang bervariasi sebagai fungsi dari perpanjangan zona disipatif (Tabel 1 ): zona disipatif balok memiliki perpanjangan 1 m, sedangkan zona disipatif untuk kolom diatur menjadi 0,6 m, sesuai dengan detail konstruksi. 23 , 24 Analisis struktur dan modal bersama dengan verifikasi seismik untuk berbagai kombinasi 3 , 23 , 24 diimplementasikan dalam kode numerik SAP2000. 38 Perincian struktur kolom, balok dan simpul berasal dari verifikasi ULS dan SLS serta prinsip desain kapasitas sesuai berbagai kode seismik LS. 23 , 24 Properti penampang kolom, balok dan simpul untuk konfigurasi desain pertama ini dirinci dalam Tabel 1 .
| Elemen | Rencanakan lokasi | Lantai | Ukuran [mm 2 ] | Batang memanjang a | Sanggurdi a |
|---|---|---|---|---|---|
| Balok | A1–A1′ | Pertama-ketiga | Ukuran 400×500 | 4 ϕ u 18 + 3 ϕ l 18 (D), 2 ϕ u 18 + 3ϕ l 18 (ND) | 2 kaki ϕ8/100 (D), 150(ND) |
| Keempat-kelima | Ukuran 400×500 | 3 ϕ u 18 + 3 ϕ l 18 (D), 2 ϕ u 18 + 3ϕ l 18 (ND) | 2 kaki ϕ8/100 (D), 150(ND) | ||
| B1-B1′ (Bahasa Indonesia) | Pertama-ketiga | Ukuran 400×500 | 5 ϕ u 18 + 3 ϕ l 18 (D), 2 ϕ u 18 + 3ϕ l 18 (ND) | 2 kaki ϕ8/100 (D), 150(ND) | |
| Keempat-kelima | Ukuran 400×500 | 4 ϕ u 18 + 3 ϕ l 18 (D), 2 ϕ u 18 + 3ϕ l 18 (ND) | 2 kaki ϕ8/100 (D), 150(ND) | ||
| A2–A’2 | Pertama-kelima | Ukuran 230×600 | 2ϕ u 14 + 2ϕ l 14 | 2 kaki ϕ8/100 | |
| A3–A’3 | |||||
| Kolom | Bahasa Indonesia: A1, B1 | Semua | Ukuran 600×500 | 10 ϕ20 | 4 kaki ϕ8/100 (D), 150(ND) |
| A2, A3, B2, B3 | Semua | Ukuran 600×700 | 16 dari 20 | 4 kaki ϕ8/100 (D), 150(ND) | |
| Simpul | Semua | Semua | 4 kaki ϕ8/50 |
D mengindikasikan zona disipatif dari elemen penahan sementara ND mengindikasikan zona non-disipatif; ϕ u dan ϕ l masing-masing merupakan tulangan longitudinal pada tali busur atas dan bawah.
Untuk konfigurasi desain kedua yang dilambangkan sebagai konfigurasi “ C + rebars ”, saran desain kontinuitas tulangan longitudinal balok bersama dengan keberadaan tulangan sisi muka dipertimbangkan. Tulangan tambahan adalah dua tingkat 2ϕ16 yang terletak di sekitar 1/3 dan 2/3 dari tinggi balok. Tulangan tambahan ditempatkan terus menerus sepanjang setiap balok di semua lima lantai. Keberadaan tulangan sisi muka, setelah verifikasi untuk ULS, SLS, dan LS seismik, mengarah pada perubahan langkah sengkang di area disipatif balok tahan seismik untuk semua lantai dari 10 hingga 7,5 cm. Karakteristik tulangan penampang baru disajikan dalam Tabel 2 .
| Elemen | Rencanakan lokasi | Tingkat lantai | Ukuran [mm 2 ] | Batang memanjang a | Sanggurdi a |
|---|---|---|---|---|---|
| Balok | A1–A1′ | Pertama-ketiga | Ukuran 400×500 | 4 ϕ kamu 18 + 3 ϕ aku 18 + 4 ϕ s 16 | 2 kaki ϕ8/ 75 (D), 150(ND) |
| Keempat-kelima | Ukuran 400×500 | 3 ϕ kamu 18 + 3 ϕ aku 18 + 4 ϕ s 16 | 2 kaki ϕ8/ 75 (D), 150(ND) | ||
| B1-B1′ (Bahasa Indonesia) | Pertama-ketiga | Ukuran 400×500 | 5 ϕ kamu 18 + 3 ϕ aku 18 + 4 ϕ s 16 | 2 kaki ϕ8/ 75 (D), 150(ND) | |
| Keempat-kelima | Ukuran 400×500 | 4 ϕ kamu 18 + 3 ϕ aku 18 + 4 ϕ s 16 | 2 kaki ϕ8/ 75 (D), 150(ND) | ||
| A2–A’2 | Pertama-kelima | Ukuran 230×600 | 2ϕ u 14 + 2ϕ l 14 | 2 kaki ϕ8/100 | |
| A3–A’3 | |||||
| Kolom | Bahasa Indonesia: A1, B1 | Semua | Ukuran 600×500 | 10 ϕ20 | 4 kaki ϕ8/ 100 (D), 150(ND) |
| A2, A3, B2, B3 | Semua | Ukuran 600×700 | 16 dari 20 | 4 kaki ϕ8/ 100 (D), 150(ND) | |
| Simpul | Semua | Semua | 4 kaki ϕ8/ 50 |
D mengindikasikan zona disipatif dari elemen penahan sementara ND mengindikasikan zona non-disipatif; ϕ u dan ϕ l masing-masing merupakan tulangan longitudinal pada tali busur atas dan bawah, dan ϕ s mengindikasikan tulangan sisi muka.
Mengenai konfigurasi struktur ketiga yang disebut sebagai konfigurasi “ CSE + tulangan ”, susunan tulangan lantai yang sama dan simetri penampang diadopsi, yang mengarah pada perubahan tata letak tulangan elemen struktur setelah verifikasi untuk ULS, SLS, dan desain kapasitas seismik. Secara khusus, peningkatan diameter sengkang pada simpul balok-kolom seluruh bangunan dari 8 menjadi 10 mm (Tabel 3 ) telah diperlukan.
| Elemen | Rencanakan lokasi | Tingkat lantai | Ukuran [mm 2 ] | Batang memanjang a | Sanggurdi a |
|---|---|---|---|---|---|
| Balok | A1–A1′ | Semua | Ukuran 400×500 | 4 ϕ kamu 18 + 4 ϕ aku 18 + 4 ϕ s 16 | 2 kaki ϕ8/ 75 (D), 150(ND) |
| B1-B1′ (Bahasa Indonesia) | Semua | Ukuran 400×500 | 5 ϕ kamu 18 + 5 ϕ aku 18 + 4 ϕ s 16 | 2 kaki ϕ8/ 75 (D), 150(ND) | |
| A2–A’2
A3–A’3 |
Semua | Ukuran 230×600 | 2 ϕ kamu 14 + 2 ϕ aku 14 + 4 ϕ s 16 | 2 kaki ϕ8/100 | |
| Kolom | Bahasa Indonesia: A1, B1 | Semua | Ukuran 600×500 | 10 ϕ20 | 4 kaki ϕ8/ 100 (D), 150(ND) |
| A2, A3, B2, B3 | Semua | Ukuran 600×700 | 16 dari 20 | 4 kaki ϕ8/ 100 (D), 150(ND) | |
| Simpul | Semua | Semua | 4 kaki ϕ10/ 50 |
D mengindikasikan zona disipatif dari elemen penahan sedangkan ND mengindikasikan zona non-disipatif; ϕ u dan ϕ l masing-masing merupakan tulangan longitudinal pada tali busur atas dan bawah, dan ϕ s mengindikasikan tulangan sisi muka.
Perlu dicatat bahwa modifikasi pada dua konfigurasi terakhir tidak diterapkan untuk balok lebar tetapi hanya untuk balok rangka MR karena balok lebar mematuhi prinsip kontinuitas dan simetri pada model “ STANDARD ”, dan tidak memiliki ruang yang cukup untuk tulangan sisi muka.
4 DEFINISI MODEL NLFE UNTUK SIMULASI SKENARIO KEGAGALAN
Bagian ini menjelaskan bagaimana model NLFE 2D dari rangka yang terlibat dalam skenario kegagalan telah ditetapkan untuk setiap konfigurasi struktural untuk mencapai kurva kapasitas 2D. Faktanya, simulasi NLFE 2D memungkinkan penilaian respons non-linier rangka RC sehubungan dengan kegagalan daktail atau getas dalam mekanisme resistensi lokal atau global. Sebaliknya, analisis FE 3D tidak dipertimbangkan karena salah satu tujuan studi ini adalah untuk menumpangkan hasil dari simulasi NLFE bidang rangka 2D yang dirancang dengan tepat untuk meningkatkan kekokohan struktur RC 3D di zona seismik. Ini bisa sangat efektif, terutama untuk struktur dengan pelat RC yang memiliki balok sepanjang hanya satu arah untuk memvalidasi bagaimana saran kekokohan telah diterapkan dalam desain seismik, khususnya rangka MR bidang. Dengan cara ini, desain struktur RC 3D dapat dilakukan melalui desain rangka MR bidang termasuk prinsip seismik dan kekokohan.
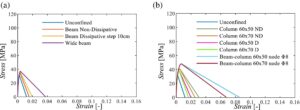
Model prediktif numerik dilakukan dengan mempertimbangkan perangkat lunak FEM ATENA 2D. 39 Semua asumsi di balik pemodelan numerik 40 – 48 telah divalidasi dengan mereproduksi hasil uji eksperimental pada subrakitan balok-kolom, 31 yang rinciannya diberikan dalam Lampiran A. Tentu saja, satu-satunya perbedaan menyangkut sifat material dan karakteristik geometris, sedangkan asumsi dan strategi pemodelan lainnya adalah sama. Secara khusus, respons tekan beton yang terkait dengan konfigurasi tulangan STANDARD, C + , dan CSE + masing-masing diilustrasikan dalam Gambar 2 – 4 yang membedakan antara elemen struktural yang berbeda karena efek pengekangan yang berbeda. Secara rinci, model konstitutif telah diformulasikan untuk: beton tak terkekang (yaitu, selimut beton efektif—“tak terkekang”), beton di daerah balok tak terdisipatif (“balok Tak Terdisipatif”), beton di daerah terdisipatif balok (“balok Terdisipatif” dengan mempertimbangkan langkah sengkang), beton di balok lebar (“balok Lebar”), beton di bagian kolom tak terdisipatif (“kolom ND”), beton di bagian terdisipatif kolom (“kolom D,” dengan mempertimbangkan langkah sengkang dan dua penampang melintang yang berbeda) dan beton di simpul balok-kolom (dengan mempertimbangkan diameter sengkang dan sifat penampang yang berbeda). Perhatikan bahwa efek pengekangan pada balok sangat penting karena, selama tahap awal mekanisme, balok dikenai gaya lengkung tekan yang menentukan beban tekan aksial yang relevan pada balok. Jika tidak dipertimbangkan, kapasitas sistem struktur akan diremehkan, seperti yang ditunjukkan dalam Lampiran A. Namun, hal ini berlaku untuk skenario di mana kolom yang hilang tidak berada di sepanjang tepi. Untuk kasus dengan kolom yang dihilangkan di sepanjang tepi, efek pengekangan pada balok tidak diperhitungkan, dan hukum konstitutifnya adalah hukum kurva “tanpa pengekangan” pada Gambar 2 – 4 .


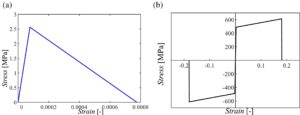
Respons tarik beton digambarkan pada Gambar 5a untuk ketiga konfigurasi, sedangkan hukum tegangan-regangan tulangan adalah kurva bi-linear, yang sama dalam tarikan dan kompresi, dan ditunjukkan pada Gambar 5b . Khususnya, rasio kekuatan luluh-terakhir ditetapkan sebesar 1,25 dan regangan akhir diasumsikan sebesar 0,18. Asumsi ini didasarkan pada banyak uji eksperimental. 28 – 31 , 49 – 53
Akhirnya, hilangnya kolom pendukung direproduksi dengan menerapkan perpindahan vertikal, dengan langkah 1 cm, di titik atas kolom yang dilepas, tanpa mempertimbangkan tindakan lain. Prosedur langkah demi langkah ini memungkinkan untuk mengevaluasi respons struktural serta deformasi dan pola retak bersama dengan kondisi tegangan, menyelidiki resistansi residual struktur (yaitu, kurva kapasitas). Pada akhirnya, kendala yang sepenuhnya tetap ditetapkan di dasar setiap kolom.
5 SKENARIO KEGAGALAN DAN KALIBRASI PER NON-LINEAR
Untuk tiga konfigurasi struktural, studi ini mengeksplorasi empat skenario kegagalan yang berbeda, seperti yang ditunjukkan pada Gambar 1 dan 6 .
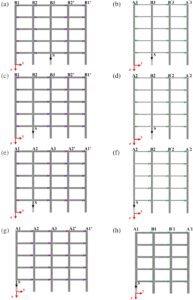
Keempat skenario kegagalan ini menggambarkan situasi relevan dan terburuk dalam bangunan di mana kontribusi apa pun yang berasal dari infill 37 tidak ada. Skenario kegagalan pertama (FS1—Gambar 1 ) melibatkan pemindahan kolom B3 dan memengaruhi rangka FS1- x dan FS1- y (Gambar 6a, b ); yang kedua (FS2—Gambar 1 ) melibatkan pemindahan kolom B2 dan memengaruhi rangka FS2- x dan FS2- y (Gambar 6c, d ); yang ketiga (FS3—Gambar 1 ) melibatkan pemindahan kolom A2 dan memengaruhi rangka FS3- x dan FS3- y (Gambar 6e, f ); yang keempat (FS4—Gambar 1 ) melibatkan pemindahan kolom A1 dan memengaruhi rangka FS4- x dan FS4- y (Gambar 6g, h ). Secara total, 24 frame berbeda dianalisis melalui analisis pushdown NLFE 2D, dengan mempertimbangkan empat FS, dua arah (yaitu, x dan y ) dalam tiga konfigurasi struktural yang berbeda. Tinjauan umum semua simulasi dalam analisis parametrik tercantum dalam Tabel 4 .
| Desain/konfigurasi struktural | Dukungan-kontinuitas dan kontribusi ortogonal | Kontinuitas | Simetri bagian | Kesetaraan lantai | Tulangan sisi muka | Skenario kegagalan | Bingkai sepanjang arah x | Bingkai sepanjang arah y |
|---|---|---|---|---|---|---|---|---|
| STANDAR | • | ○ | ○ | ○ | ○ | FS1, FS2, FS3, FS4 | ✔ | ✔ |
| CSE + tulangan | • | • | • | • | • | FS1, FS2, FS3, FS4 | ✔ | ✔ |
| Tulangan C+ | • | • | ○ | ○ | • | FS1, FS2, FS3, FS4 | ✔ | ✔ |
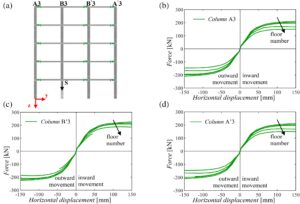
Dengan tujuan untuk mengembangkan beberapa simulasi NLFE, hukum konstitutif pegas non-linier horizontal lateral (Gambar 6 ) harus didefinisikan secara spesifik. Faktanya, komponen struktural ortogonal terhadap setiap rangka 2D yang dianalisis secara signifikan meningkatkan kekakuan struktur, yang memaksakan pembatasan pada perpindahan lateral. 11 , 12 , 16 – 18 Pengabaian kekakuan rotasi dibenarkan oleh efek minimalnya pada puncak lentur dan dampaknya yang dapat diabaikan pada pengembangan aksi katenari, seperti yang ditekankan dalam Pham dan Tan, 16 Tan et al. 54 Untuk mensimulasikan kontribusi yang diberikan oleh rangka ortogonal terhadap rangka yang dianalisis, pegas non-linier translasi telah ditempatkan di setiap simpul dari lima lantai, seperti yang ditunjukkan, misalnya, pada Gambar 7b untuk rangka FS1- x (yaitu, untuk skenario kegagalan pertama dalam arah x ).
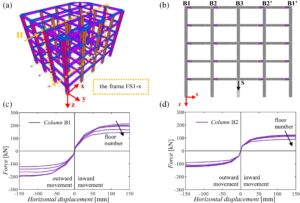
Hukum non-linier konstitutif pegas translasi dikalibrasi dengan tepat melalui analisis non-linier dalam SAP2000 38 yang dilakukan pada struktur RC 3D. Pertama, kolom pendukung telah dihilangkan untuk mensimulasikan skenario kegagalan spesifik dan kekakuan aksial dan lentur balok dan kolom rangka yang dipelajari dinetralisir karena kontribusinya diperhitungkan dalam model NLFE 2D (misalnya, pada Gambar 7b ). Perilaku non-linier rangka dalam struktur 3D telah dimodelkan menggunakan engsel plastik berbasis serat yang ditempatkan pada titik-titik tertentu di kolom dan balok. Panjang engsel plastik telah dihitung berdasarkan 55 , 56 dengan mempertimbangkan karakteristik geometris penampang elemen struktural. Secara rinci, panjang engsel plastik sekitar 50 cm untuk balok dan 30 cm untuk kolom. Sementara itu, jumlah serat untuk setiap penampang telah ditentukan melalui proses iteratif untuk memastikan akurasi numerik. Secara spesifik, engsel serat plastik yang digunakan dalam model tersebut adalah tipe “P-M2-M3”, yang memperhitungkan gaya aksial dan dua momen lentur ortogonal.
Dalam simulasi 3D, non-linieritas geometri juga dipertimbangkan. Kontribusi yang diberikan oleh pelat yang memiliki balok satu arah (karakteristik umum konstruksi Eropa) diabaikan seperti yang ditandai dalam Scalvenzi et al. 10 Hukum konstitutif dari kedua material, yang diadopsi dalam model 3D, telah dijelaskan dalam Bagian 4. Kemudian, analisis numerik yang dikontrol perpindahan telah dilakukan dengan memaksakan, dalam setiap node, perpindahan horizontal ( H ) dalam arah keluar bidang dari rangka ortogonal (misalnya, arah x positif untuk contoh yang dilaporkan dalam Gambar 7a ) dengan langkah 1 cm. Lebih jauh, hukum konstitutif telah dikalibrasi untuk arah dalam dan luar, menunjukkan perbedaan, sedikit lebih jelas di lantai yang lebih tinggi, antara perilaku dalam dua arah yang berlawanan. Perhatikan bahwa kalibrasi untuk kedua arah dapat lebih relevan ketika strukturnya tidak simetris (misalnya, keberadaan tangga atau dinding pengisi dalam skema yang tidak simetris). Setiap hukum konstitutif non-linier diperoleh dengan memplot gaya pada simpul yang dianalisis terhadap perpindahan horizontal yang dikenakan. Proses ini telah diulangi untuk setiap simpul di semua kolom kecuali yang mengalami keruntuhan dan untuk setiap konfigurasi struktural dan skenario kegagalan. Kegagalan geser tidak pernah tercapai, dengan menghormati semua verifikasi geser. Perpindahan horizontal maksimum yang dikenakan sebesar 150 mm dipertimbangkan karena simpul balok-kolom tidak mengalami perpindahan yang lebih besar selama skenario keruntuhan, seperti yang ditunjukkan pada bagian berikutnya. Sebagai contoh, hukum konstitutif non-linier dilaporkan dalam Gambar 7c, d dan 8b–d untuk konfigurasi ” STANDARD ” dan skenario kegagalan pertama di sepanjang, masing-masing, arah x dan y . Perlu dicatat juga bahwa pegas memasuki medan non-linier untuk perpindahan horizontal yang lebih besar dari sekitar 20 mm.
6 SKENARIO KEGAGALAN PERTAMA: HASIL NUMERIK DAN PERBANDINGAN
Bagian ini menjelaskan pemindahan kolom B3, yang diindikasikan sebagai skenario kegagalan pertama FS1. Untuk skenario kegagalan ini dan tiga konfigurasi desain, hukum konstitutif untuk pegas non-linier telah dikalibrasi, seperti yang dijelaskan sebelumnya di Bagian 5 .
6.1 Analisis NLFE sepanjang arah x
Subbagian ini menggambarkan kurva kapasitas dari tiga konfigurasi rangka FS1- x , yang memiliki balok dalam dan mengalami pelepasan kolom B3 (yaitu, skenario kegagalan pertama, Gambar 6a ).
Kurva kapasitas yang terkait dengan konfigurasi “ STANDARD ”, disajikan pada Gambar 9a , menunjukkan beban tahan maksimum pada fase lentur (yaitu,
) sama dengan 1129 kN. Setelah itu, kurva kapasitas menunjukkan fase pelunakan awal diikuti oleh permulaan efek katenari untuk perpindahan yang sangat besar (yaitu, sekitar 60 cm) yang terlihat juga dari perpindahan horizontal simpul balok-kolom (Gambar 9b ) dengan peningkatan yang sangat sedikit dalam resistensi struktural. Peningkatan berhenti ketika batang mencapai regangan ultimitnya, dan ini terjadi pada beban ultimit maksimum (yaitu, P MAX,ULT ) sama dengan 1024 kN, dengan perpindahan vertikal yang dikenakan sekitar 64 cm. Perpindahan vertikal simpul di kedua kolom B1 dan B2 (Gambar 9c ) menunjukkan penurunan diikuti oleh peningkatan. Pengurangan awal adalah hasil dari perilaku melengkung balok, sedangkan peningkatan berikutnya terjadi karena rotasi simpul dalam transisi ke aktivasi katenari.
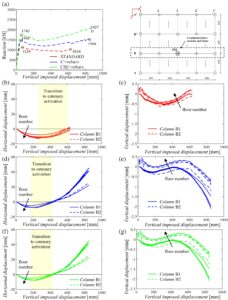
Rekomendasi desain dalam konfigurasi ” C + rebars” , khususnya, kontinuitas tulangan longitudinal balok dan penyertaan tulangan sisi muka, menghasilkan keuntungan yang signifikan, seperti yang ditunjukkan oleh kurva kapasitas bersama dengan perpindahan horizontal dan vertikal dari simpul-simpul pada Gambar 9a, d, e . Transisi menuju fase katenari sangat diantisipasi (yaitu, pada perpindahan vertikal lebih rendah dari 20 cm). Peningkatan ini terbukti dalam kurva kapasitas dan perpindahan horizontal dari simpul-simpul balok-kolom, di mana perubahan tanda disorot. Manfaat ini dijamin oleh kedua perbaikan desain: tulangan, yang memiliki susunan yang lebih panjang di sepanjang balok, berkontribusi untuk membangun efek ikatan pada perpindahan vertikal awal; tulangan sisi muka, yang ditempatkan di bagian tengah penampang, mengalami regangan rendah selama fase lentur, dan ini membantu mengantisipasi perilaku katenari ketika gaya tarik muncul. Dengan mengamati perpindahan horizontal dari simpul balok-kolom (Gambar 9b, d, f ), pegas memasuki rezim non-linier ketika perpindahan vertikal yang dikenakan lebih besar dari 60 cm (yaitu, ketika efek catenary sudah diaktifkan) dan hanya sepanjang arah ke dalam, sedangkan selama fase lengkungan-lentur dan pelunakan, non-linieritas tidak dimanfaatkan.
Dengan demikian, kalibrasi nonlinier untuk kontribusi rangka ortogonal sangat penting, terutama ketika fenomena dinamis melibatkan perpindahan besar. Selain itu, ada peningkatan baik dalam beban tahan maksimum selama fase lentur dan beban tahan ultimit, karena jumlah tulangan yang lebih besar di balok. Keuntungan penting terakhir terkait dengan daktilitas karena regangan ultimit untuk tulangan longitudinal (yaitu, 18%) dicapai pada perpindahan vertikal yang dikenakan lebih dari 20 cm kemudian dibandingkan dengan konfigurasi tanpa tulangan sisi muka. Konfigurasi ” CSE + tulangan ” menambahkan kesetaraan dalam pengaturan tulangan antara lantai dan simetri penampang. Ini mengarah pada peningkatan jumlah tulangan dengan perbaikan berikut: baik puncak lentur dan ketahanan ultimit menunjukkan nilai yang lebih tinggi dan efek katenari sedikit diantisipasi dibandingkan dengan konfigurasi sebelumnya (yaitu, tulangan C + ), seperti yang terlihat pada Gambar 9a . Tulangan longitudinal mencapai regangan ultimit (yaitu, 18%) pada perpindahan vertikal yang dikenakan sama dengan 90 cm.
6.2 Analisis NLFE sepanjang arah y
Analisis pushdown telah dinilai untuk rangka FS1- y , yang merupakan rangka yang memiliki balok lebar dan mengalami pemindahan kolom B3 (yaitu, skenario kegagalan pertama) sepanjang arah y , seperti dijelaskan dalam Gambar 6b . Gambar 10 melaporkan kurva kapasitas bersama dengan perpindahan vertikal dan horizontal dari simpul balok-kolom. Hasil dalam bentuk kurva kapasitas menunjukkan perilaku yang sepenuhnya berbeda dari kurva kapasitas yang diilustrasikan dalam Bagian 6.1 . Dalam kasus ini, mengenai tiga solusi desain, fase lentur diakhiri dengan beban tahan maksimum yang sama dengan 159 kN, yang secara signifikan lebih rendah (Gambar 10a ). Perbedaan ini bergantung pada jumlah tulangan yang lebih rendah pada balok lebar (yaitu, 2 ϕ14 pada tali busur atas dan 2 ϕ14 pada tali busur bawah penampang melintang). Kurva menunjukkan transisi aktivasi katenari yang terjadi antara 15 dan 20 cm dari perpindahan vertikal yang dikenakan, dengan demikian secara signifikan mengantisipasi fase katenari. Fase katenari tidak hanya diantisipasi tetapi secara signifikan lebih jelas dengan beban tahan maksimum yang jauh lebih besar daripada yang tercatat pada puncak lentur. Hal ini dapat dikaitkan dengan alasan-alasan berikut: (i) tulangan longitudinal balok lebar kontinu sepanjang elemen struktural dimulai dari konfigurasi STANDARD , dan ini membantu mengembangkan efek ikatan; (ii) balok lebar secara signifikan lebih daktail daripada balok dalam. 37 Dengan mengamati perpindahan horizontal simpul balok-kolom (Gambar 10b, d, f ), pegas memasuki rezim non-linier ketika perpindahan vertikal yang dikenakan lebih besar dari 35 cm (yaitu, ketika efek katenari sudah dimobilisasi). Dengan demikian, medan non-linier untuk pegas translasi dicapai lebih awal untuk rangka dalam arah y dibandingkan dengan rangka dalam arah x . Untuk alasan ini, kalibrasi non-linier dari hukum pegas sangat penting. Sekali lagi, non-linieritas tidak terlibat selama pergerakan keluar dari simpul balok-kolom (yaitu, fase lengkungan-lentur dan fase pelunakan) tetapi hanya untuk pergerakan ke dalam (yaitu, fase katenari).
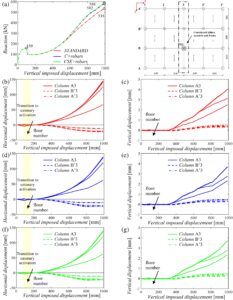
Dari kurva kapasitas ini, dapat juga diamati bahwa hanya ada sedikit perbedaan antara konfigurasi tulangan STANDARD , C+ dan tulangan CSE+ karena balok lebar tidak mengalami modifikasi desain yang berbeda. Perbedaan minimal dalam hasil disebabkan oleh pegas translasi non-linier, yang dikalibrasi ulang dengan mempertimbangkan perbaikan desain pada elemen struktural lainnya (yaitu, tulangan longitudinal dan transversal balok dan sengkang sambungan) bangunan 3D dalam konfigurasi tulangan C+ dan tulangan CSE+ . Faktanya, perbedaan tersebut dapat diperhatikan pada perpindahan vertikal yang sangat besar.
6.3 Superposisi kurva kapasitas
Gagasan yang diusulkan dari Bagian 2 adalah untuk menumpangkan kurva kapasitas NLFE 2D guna memperoleh kurva kapasitas global yang sesuai yang menggambarkan perilaku yang ditunjukkan oleh rangka 3D untuk hilangnya kolom. Untuk mencapai hal ini, kurva kapasitas yang diperoleh untuk dua rangka, yang saling ortogonal, yang mengalami hilangnya kolom yang sama dalam skenario keruntuhan pertama FS1 (yaitu, kolom B3) ditumpangkan, sebagaimana juga dilakukan secara eksperimental untuk substruktur dalam Tan et al. 54 Prosedur ini telah diulang untuk tiga konfigurasi yang berbeda guna membandingkan keuntungan dari saran desain.
Dari Gambar 11 , dapat disimpulkan bagaimana rangka FS1- y (yaitu, rangka dengan balok lebar), yang menghadirkan puncak lentur yang jauh lebih rendah daripada rangka FS1- x , menawarkan kontribusi minimal dalam fase lentur hingga beban tahan maksimum. Kontribusi ini secara bertahap meningkat untuk perpindahan yang lebih besar karena daktilitas rangka dengan balok lebar yang lebih besar, seperti dijelaskan dalam Bagian 6.2 . Perilaku ini ditunjukkan dalam kurva kapasitas yang ditumpangkan untuk ketiga konfigurasi. Selain itu, untuk semua konfigurasi struktural, rangka sepanjang arah y mengarah pada transisi menuju aktivasi katenari untuk perpindahan vertikal yang lebih kecil dengan resistensi ultimit (diatur oleh kegagalan rangka FS1- x ) yang lebih besar daripada puncak lentur (yaitu, Gambar 11 ). Perbaikan terakhir ini khususnya terbukti dalam konfigurasi tulangan C + dan tulangan CSE + (yaitu, masing-masing 1990 dan 2200 kN, yang lebih tinggi daripada puncak lentur yang masing-masing sebesar 1600 dan 1900 kN). Ini memastikan tingkat keamanan yang lebih tinggi jika terjadi peristiwa yang melibatkan hilangnya kolom untuk kedua konfigurasi ini. Kurva kapasitas global, untuk konfigurasi STANDARD (Gambar 11a ), menunjukkan penurunan vertikal diikuti oleh peningkatan resistensi pada sekitar 60 cm. Tren ini disebabkan oleh mengatasi regangan ultimit pada tulangan longitudinal balok (yaitu, 18%) dalam rangka sepanjang arah- x (yaitu, rangka tahan seismik). Setelah itu, satu-satunya kontribusi datang dari rangka ortogonal dalam arah -y . Tren ini sama untuk model tulangan C+ (Gambar 11b ) dan tulangan CSE+ (Gambar 11c ), tetapi dengan perpindahan vertikal akhir yang lebih besar (yaitu, masing-masing 87 dan 89 cm).
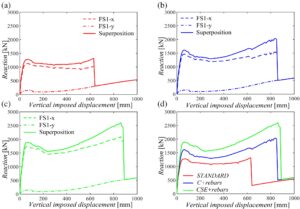
Dari perbandingan tersebut, dapat disimpulkan bahwa, untuk skenario kegagalan pertama, model dengan kontinuitas tulangan longitudinal balok dan keberadaan tulangan sisi muka (yaitu, konfigurasi tulangan C+ ) menunjukkan keseimbangan terbaik antara peningkatan kekokohan struktur dan prinsip keberlanjutan, karena jumlah tulangan longitudinal yang disusun lebih sedikit.
6.4 Perbandingan dengan model 3D
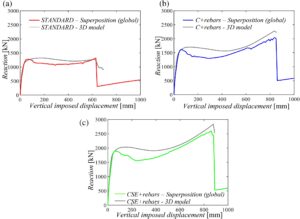
Untuk mengkaji efektivitas kurva kapasitas global yang diperoleh melalui superposisi analisis NLFE 2D pada dua rangka ortogonal yang terpengaruh oleh skenario kegagalan pertama, analisis non-linier dorong-turun yang dikontrol perpindahan 3D telah dilakukan pada model 3D dalam SAP2000, 38 yang didefinisikan dalam Bagian 5. Hukum konstitutif dari kedua material yang diadopsi dalam model 3D dijelaskan dalam Bagian 4. Analisis tersebut terdiri dari penerapan perpindahan vertikal yang meningkat, dengan langkah 1 cm, di bagian atas kolom pendukung yang dilepas (yaitu, kolom B3), dan menentukan gaya yang diberikan oleh struktur yang tersisa pada titik spesifik tersebut. Dalam simulasi 3D, non-linieritas geometris juga dipertimbangkan. Perhatikan bahwa non-linieritas terkonsentrasi di balok dan kolom rangka melalui engsel plastik serat, seperti dijelaskan dalam Bagian 5 .
Pada Gambar 12 , kurva kapasitas 3D yang diperoleh dari model 3D dibandingkan dengan kurva kapasitas global yang diperoleh dari superposisi analisis NLFE 2D. Perbedaan utamanya adalah pada tahap pelunakan, dengan pengurangan resistansi yang lebih rendah pada model 3D. Aspek ini berasal dari perbedaan pemodelan antara kode perangkat lunak yang digunakan. Dalam kasus analisis statis non-linier yang dilakukan pada model 3D, non-linieritas struktur terkonsentrasi pada engsel plastik berbasis serat, yang hanya mempertimbangkan interaksi antara gaya aksial dan momen lentur, mengabaikan interaksi dengan gaya geser, bersama dengan pemodelan yang berbeda dari evolusi retak beton. Selain itu, keberadaan sengkang tidak dimodelkan dalam model 3D, tetapi hanya efek pengekangan yang disertakan, sedangkan dalam analisis NLFE, sengkang dimodelkan sebagai elemen rangka diskret. Akan tetapi, dapat diperhatikan bahwa puncak lentur, misalnya, dalam model STANDARD 3D sama dengan 1280 kN, yang sangat mirip dengan nilai yang diperoleh dalam kurva kapasitas global (yaitu, 1284 kN). Perpanjangan fase pelunakan dan fase katenari juga cukup identik. Penurunan akhir dalam resistansi juga terjadi untuk kedua model pada nilai perpindahan vertikal yang sama. Oleh karena itu, kurva kapasitas global yang dievaluasi dengan prinsip superposisi meremehkan reaksi terhadap model 3D, yang menyiratkan hasil pada sisi keamanan. Sebagai kesimpulan, hasil tersebut mengonfirmasi efektivitas superposisi kurva kapasitas 2D, yang dicapai dengan upaya komputasi yang dikurangi. Perbedaan tersebut termasuk dalam topik ketidakpastian epistemik. 57 – 60 Superposisi dalam medan non-linier hanya gagal untuk kolom yang mengalami kerugian, tetapi elemen struktural lainnya bekerja sama dengan menghormati kompatibilitas deformabilitas, seperti yang juga ditunjukkan dalam Wang et al. 19
7 SKENARIO KEGAGALAN KEDUA: HASIL NUMERIK DAN PERBANDINGAN
Bagian ini menjelaskan pemindahan kolom B2, yang diindikasikan sebagai skenario kegagalan kedua FS2. Untuk skenario kegagalan ini dan tiga konfigurasi struktural, hukum konstitutif untuk pegas non-linier telah dikalibrasi ulang mengikuti metode yang dijelaskan di Bagian 5 .
7.1 Analisis NLFE: Superposisi kurva kapasitas sepanjang arah x dan y
Kurva kapasitas rangka FS2- x dan FS2 -y ditunjukkan pada Gambar 13 untuk ketiga konfigurasi desain. Hasil yang lebih rinci dalam hal perpindahan horizontal dan vertikal dari simpul balok-kolom diberikan dalam Lampiran B (Gambar B1 dan B2).
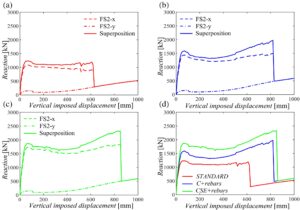
Untuk rangka dengan balok dalam sepanjang arah- x , konfigurasi STANDARD (Gambar 13a ) menunjukkan puncak lentur dan tahanan ultimit yang lebih rendah dibandingkan dengan skenario keruntuhan pertama, dan juga tidak adanya efek katenari. Hal ini karena kontribusi yang berkurang dari rangka ortogonal pada skenario keruntuhan kedua. Kita dapat memahami bagaimana keberadaan tulangan sisi muka pada konfigurasi tulangan C + (Gambar 13b ), sama seperti skenario keruntuhan pertama, menyebabkan peningkatan puncak lentur dan memudahkan pengaktifan efek katenari (pada perpindahan sekitar 20 cm). Kesimpulan serupa dapat ditarik terkait konfigurasi tulangan CSE + (Gambar 13c ).
Kurva kapasitas, yang diperoleh untuk rangka dengan balok lebar sepanjang arah y (yaitu, FS2- y ), serupa dengan yang dilaporkan dalam Bagian 6.2 : fase lentur secara signifikan lebih rendah dibandingkan dengan nilai yang dicapai untuk rangka yang runtuh ortogonal, tetapi transisi katenari sangat diantisipasi dan lebih jelas. Membandingkan kurva kapasitas global (Gambar 13d ), konfigurasi CSE + tulangan menunjukkan peningkatan lentur dan ketahanan ultimit dibandingkan dengan konfigurasi C + tulangan , juga dengan perpindahan vertikal yang lebih tinggi saat runtuh.
Bahkan dalam skenario kegagalan ini, konfigurasi tulangan C + menunjukkan keseimbangan optimal antara peningkatan kekokohan struktural dan peningkatan keberlanjutan. Lebih jauh lagi, seperti yang juga terlihat di Lampiran B (Gambar B1 dan B2 ), kalibrasi pegas translasi non-linier dapat menjadi krusial untuk skenario kegagalan ini untuk menangkap respons juga selama fase lengkung-lentur awal untuk rangka dalam arah x (Gambar B1 ) tetapi khususnya pada perpindahan besar (yaitu, fase katenari) untuk kedua rangka (Gambar B1 dan Gambar B2 ). Faktanya, simpul balok-kolom rangka F2- x dan, khususnya, rangka F2- y mengalami perpindahan horizontal lebih besar dari 20 mm (yaitu, nilai di mana non-linieritas pegas translasi diaktifkan) baik untuk gerakan ke dalam maupun ke luar.
7.2 Perbandingan dengan model 3D
Juga untuk menghilangkan kolom B2 (yaitu, skenario kegagalan kedua), analisis dorong ke bawah yang dikontrol perpindahan telah dilakukan pada struktur 3D di SAP2000, 38 seperti yang ditunjukkan pada Gambar 14 .

Temuan yang sebanding dapat diperoleh untuk skenario kegagalan kedua: puncak lentur dalam model 3D sangat mencerminkan nilai kurva kapasitas global bahkan jika pada perpindahan vertikal sedikit lebih tinggi dalam model 3D; transisi melalui efek katenari cukup bersamaan serta penurunan akhir dalam resistansi terjadi pada perpindahan vertikal yang identik dan hasil pendekatan yang ditumpangkan berada di sisi yang aman jika dibandingkan dengan model 3D. Karena FS kedua lebih menuntut dalam hal tegangan lokal, perbedaan yang lebih tinggi antara kurva global dan 3D berada dalam fase pelunakan karena retak dan hancurnya beton. Namun, hasil ini mengonfirmasi efektivitas superposisi kurva kapasitas 2D juga untuk FS kedua.
8 SKENARIO KEGAGALAN KETIGA: HASIL NUMERIK DAN PERBANDINGAN
Bagian ini membahas skenario kegagalan ketiga FS3 (yaitu, pelepasan kolom A2) untuk konfigurasi STANDARD , C + tulangan , dan CSE + tulangan . Hukum konstitutif yang mengatur pegas non-linier telah dikalibrasi ulang menggunakan pendekatan yang diuraikan dalam Bagian 5 .
8.1 Analisis NLFE: Superposisi kurva kapasitas sepanjang arah x dan y
Kurva kapasitas global untuk rangka FS3- x dan FS3- y dilaporkan dalam Gambar 15 untuk tiga konfigurasi struktural. Hasil yang lebih rinci dalam hal perpindahan horizontal dan vertikal dari simpul balok-kolom diberikan dalam Lampiran B (Gambar B3 dan B4 ). Hasil-hasil ini menggarisbawahi bahwa kalibrasi pegas non-linier dapat relevan untuk skenario kegagalan ini ketika kolom yang dilepas bukan merupakan kolom perimetral (yaitu, untuk rangka dalam arah x ) dan untuk gerakan keluar dan, terutama, gerakan ke dalam dari simpul balok-kolom. Secara berbeda, untuk rangka dalam arah y , perpindahan horizontal dari simpul balok-kolom sangat rendah (yaitu, jauh lebih rendah dari 20 mm) dan pegas tetap dalam rezim linier. Rangka pada arah- x , yang memiliki balok-balok dalam dan mengalami keruntuhan, tidak seperti yang diamati pada dua skenario keruntuhan pertama, merupakan rangka perimeter (yaitu, rangka FS3- x ), dan balok-balok memiliki jumlah tulangan longitudinal yang sedikit lebih rendah dibandingkan dengan rangka FS1- x dan FS2- x , seperti yang dilaporkan dalam Tabel 1 . Kurva kapasitas yang dilaporkan dalam Gambar 15 menunjukkan, dalam konfigurasi STANDARD , puncak lentur terendah di antara tiga kasus yang dianalisis dan tidak adanya efek katenari. Meningkatnya keberadaan batang menghasilkan peningkatan puncak lentur, seperti yang diamati dalam konfigurasi tulangan C + dan tulangan CSE + . Transisi menuju efek katenari hadir dalam konfigurasi tulangan C + dan tulangan CSE + . Pada rangka FS3- y , yang memiliki balok lebar, hanya sedikit efek katenari yang diamati, dimulai sekitar 20 cm perpindahan vertikal yang dikenakan. Kontribusi rangka FS3 -y sangat berkurang sehubungan dengan skenario keruntuhan pertama dan kedua. Perlu dicatat bahwa, untuk rangka FS3- y , efek pengekangan pada balok dalam hal hukum konstitutif beton dalam kompresi tidak disertakan karena kegagalan melibatkan kolom perimeter (yaitu, kolom A2). Oleh karena itu, mekanisme penahan terutama bergantung pada balok ortogonal. Bahkan dalam kasus ini, konfigurasi tulangan C + merupakan pilihan yang tepat antara meningkatkan kekokohan struktural dan mempromosikan keberlanjutan.
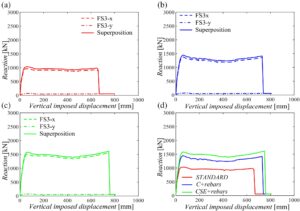
8.2 Perbandingan dengan model 3D
Gambar 16 menggambarkan perbandingan antara kurva kapasitas global yang diperoleh pada subbagian sebelumnya dan kurva kapasitas 3D yang diperoleh pada struktur 3D di SAP2000. 38
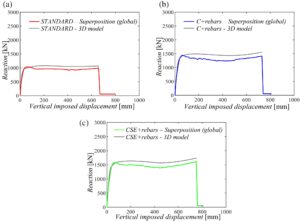
Juga untuk skenario kegagalan ketiga, analisis nonlinier dorong-turun yang dikontrol perpindahan 3D telah dilakukan setelah pelepasan kolom A2, dengan mengabaikan efek pengekangan pada balok sebagaimana dilakukan untuk kurva kapasitas global. Puncak lentur serupa, meskipun terjadi pada perpindahan vertikal yang sedikit lebih tinggi pada kurva 3D. Efek katenari serupa dan pengurangan resistansi terjadi pada perpindahan vertikal yang sama. Sekali lagi, hasil superposisi yang diusulkan dikonfirmasi dan berada di sisi yang aman.
8.3 Skenario kegagalan keempat: Hasil numerik dan perbandingan
Bagian ini menjelaskan skenario keruntuhan keempat FS4, yang melibatkan pemindahan kolom A1, untuk konfigurasi tulangan STANDARD , C + , dan CSE + . Hukum pegas non-linier telah dikalibrasi ulang mengikuti metodologi yang dirinci dalam Bagian 5 .
8.4 Analisis NLFE: Superposisi kurva kapasitas sepanjang arah x dan y
Kurva kapasitas yang terkait dengan arah x dan y serta superposisi dilaporkan dalam Gambar 17. Hasil yang lebih rinci dalam hal perpindahan horizontal dan vertikal dari simpul balok-kolom diberikan dalam Lampiran B (Gambar B5 dan B6 ).
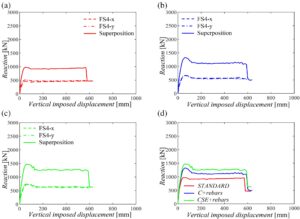
Pada gambar Lampiran B ini , ditunjukkan bagaimana kalibrasi pegas non-linier tidak begitu relevan untuk skenario kegagalan ini karena perpindahan horizontal simpul balok-kolom di kedua rangka jauh lebih rendah dari 20 mm dan pegas tetap dalam rezim linier. Hal ini disebabkan oleh fakta bahwa kolom yang dilepas merupakan kolom perimetral untuk kedua rangka sepanjang arah x dan y .
Rangka FS4- x bersifat perimetral dan memiliki balok dalam dengan jumlah tulangan longitudinal yang sedikit lebih rendah dibandingkan dengan rangka FS1- x dan FS2- x dan sama dengan rangka FS3- x . Namun, kolom yang dihilangkan adalah kolom samping seperti yang ditunjukkan pada Gambar 6g . Kurva kapasitas mengungkapkan bahwa konfigurasi STANDARD menunjukkan puncak lentur terkecil, tidak adanya efek katenari, dan resistansi menunjukkan dataran tinggi hingga regangan pamungkas untuk tulangan longitudinal (yaitu, 18%) pada sekitar 60 cm perpindahan vertikal yang dikenakan. Khususnya, kurva kapasitas yang terkait dengan konfigurasi yang ditingkatkan dicirikan oleh puncak lentur yang lebih besar sehubungan dengan kasus STANDARD . Ini menyiratkan energi internal yang lebih tinggi dan, dengan demikian, kemampuan untuk menemukan titik kinerja (seperti yang dijelaskan dalam Bagian 2 ) untuk perpindahan vertikal yang dikenakan lebih rendah. Kurva kapasitas dalam arah y berbeda dari kurva untuk tiga skenario keruntuhan pertama karena balok FS4- y memiliki dimensi 40 × 50 cm (yaitu, balok dalam). Dengan demikian, kurva kapasitas dalam arah x dan y untuk skenario kegagalan ini sangat mirip. Perlu dicatat bahwa kedua rangka FS4- x dan FS4 -y mengalami skenario kegagalan yang melibatkan kolom perimetral dan, dengan demikian, efek pengekangan pada balok dalam hal hukum konstitutif beton dalam kompresi tidak dimodelkan. Sekali lagi, konfigurasi tulangan C + menunjukkan keseimbangan yang baik antara peningkatan kekokohan struktural dan peningkatan keberlanjutan.
8.5 Perbandingan dengan model 3D
Gambar 18 mengilustrasikan perbandingan antara kurva kapasitas global yang diperoleh pada subbagian sebelumnya dan kurva kapasitas yang diperoleh dari analisis non-linier pushdown yang dikontrol perpindahan pada struktur 3D di SAP2000, 38 dengan mengabaikan efek pengekangan.
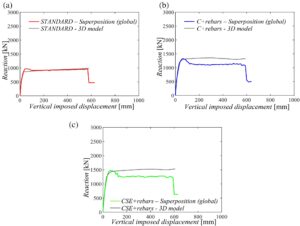
Bahkan jika resistansi akhir tercapai untuk nilai perpindahan vertikal yang sama, terdapat beberapa perbedaan dalam resistansi akhir. Hal ini disebabkan oleh keretakan pada beton serta ketidakpastian model dalam kedua pendekatan numerik. Namun, hasil ini mengonfirmasi kesesuaian yang baik antara kurva kapasitas global dan 3D juga untuk FS keempat meskipun yang pertama menghasilkan hasil yang lebih aman selain dari prediksi puncak lentur yang dicapai dalam model STANDARD .
9 PENDEKATAN ENERGETIK UNTUK EMPAT SKENARIO KEGAGALAN
Menurut pendekatan energetik oleh Izzuddin 27 yang dibahas dalam Bagian 2 , titik kinerja karena pelepasan kolom yang tidak disengaja tercapai ketika kerja eksternal W ext , yaitu, kerja yang dilakukan oleh beban gravitasi, sama dengan energi internal U i , yaitu, energi yang diserap oleh struktur. Yang pertama dihitung sebagai produk antara beban gravitasi yang terkonsentrasi di titik pelepasan kolom dan perpindahan vertikal di titik yang sama. Energi internal U i sama dengan luas di bawah kurva kapasitas global.
Gambar 19 menunjukkan perbandingan antara energi internal dan kerja eksternal dalam hal titik kinerja untuk tiga konfigurasi desain yang berbeda dan empat skenario kegagalan yang berbeda. Seperti yang dapat diamati, untuk skenario kegagalan pertama (Gambar 19a ) dan kedua (Gambar 19b ), kinerja tidak pernah tercapai untuk konfigurasi STANDARD , sementara itu tercapai untuk perpindahan vertikal antara 5 dan 10 cm untuk dua konfigurasi struktural lainnya. Selain itu, penting untuk dicatat bahwa untuk skenario kegagalan ketiga (Gambar 19c ) dan keempat (Gambar 19d ), bahkan jika keberadaan dinding pengisi dihilangkan dalam model struktural, tetapi dianggap sebagai beban eksternal, keseimbangan energi selalu diperoleh. Faktanya, dalam kasus ini, pekerjaan eksternal lebih rendah karena besarnya area efektif yang lebih rendah sehubungan dengan dua skenario pertama. Ini sejalan dengan pertimbangan dalam Caredda et al. 61 ; Faktanya, kegagalan yang berasal dari area internal umumnya memberikan beban horizontal yang lebih besar pada struktur yang tersisa daripada yang ada di zona tepi atau sudut, karena mereka memengaruhi area pengaruh keruntuhan yang lebih besar.
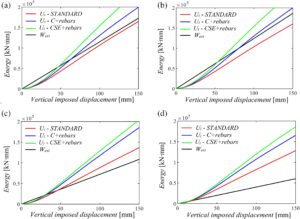
Perlu digarisbawahi bahwa kalibrasi pegas non-linier sangat penting untuk menentukan perilaku struktur 3D ketika tujuannya adalah untuk menangkap efek non-linier (yaitu, tahap pelunakan dan katenari) dan dapat menjadi penting juga untuk titik kinerja untuk beberapa konfigurasi desain dan skenario kegagalan (misalnya, FS3) meskipun perpindahan vertikal sangat rendah di semua skenario kegagalan.
Analisis energetik ini mengarah pada pendefinisian konfigurasi tulangan C+ sebagai keseimbangan optimal antara peningkatan kekokohan struktural dan peningkatan keberlanjutan, yang merupakan aspek kunci dalam terjadinya peristiwa ekstrem.
10 KESIMPULAN
Karya ini menjelaskan penilaian ketahanan struktur RC MR 3D biasa dengan mempelajari respons rangka bidang ortogonal yang terlibat dalam skenario kegagalan yang sama. Bangunan-bangunan tersebut, yang memiliki pelat dengan balok satu arah, berada di zona seismik tinggi dan dicirikan oleh rangka yang tidak tahan seismik dengan balok lebar dan rangka yang tahan seismik dengan balok dalam. Secara rinci, ketiga bangunan tersebut sesuai dengan tiga konfigurasi struktural yang berbeda: konfigurasi yang dirancang sesuai dengan aturan kode aktual dan dua konfigurasi lainnya di mana tata letak tulangan longitudinal balok dimodifikasi sesuai dengan rekomendasi ketahanan (yaitu, termasuk jumlah tulangan simetris antara tali busur bawah dan atas, kontinuitas, kriteria Vierendeel, dan tulangan sisi muka). Untuk masing-masing dari tiga konfigurasi desain, empat skenario kegagalan yang berbeda dipelajari, yang melibatkan pemindahan kolom pendukung tengah dan lateral. Untuk setiap skenario kegagalan dan konfigurasi struktural, simulasi NLFE 2D dilakukan dengan mempelajari respons rangka dalam dua arah ortogonal terhadap kolom yang gagal. Dalam simulasi NLFE 2D apa pun, kontribusi rangka yang terletak di sepanjang arah ortogonal keluar bidang dipertimbangkan melalui pegas translasi yang memiliki hukum konstitutif nonlinier dan ditempatkan di setiap simpul balok-kolom rangka bidang yang sedang diselidiki. Hubungan gaya-perpindahan pegas ini dikalibrasi melalui analisis nonlinier berbasis serat 3D dengan membuang kolom pendukung, menerapkan perpindahan translasi yang meningkat di sepanjang arah luar dan dalam di setiap simpul balok-kolom, yang menunjukkan beberapa perbedaan antara kedua arah di lantai yang lebih tinggi. Setelah kalibrasi pegas, perpindahan yang meningkat di bagian atas kolom yang dibuang diberlakukan dalam model NLFE 2D untuk menentukan kurva kapasitas bidang yang sesuai (yaitu, kurva reaksi-perpindahan). Secara berurutan, dua kurva kapasitas NLFE bidang ditumpangkan untuk menentukan kurva kapasitas global setiap struktur untuk setiap skenario kegagalan.
Kesimpulan yang dapat diambil adalah sebagai berikut:
- Hasilnya telah menunjukkan pentingnya mengkalibrasi hukum konstitutif nonlinier untuk pegas, terutama untuk beberapa skenario kegagalan serta untuk perpindahan vertikal yang besar (yaitu, setelah tahap pelunakan) ketika kolom yang dilepas bukan kolom perimetral. Hal ini penting untuk menangkap respons katenari, terutama untuk balok lebar yang memberikan kontribusi penting dalam hal duktilitas. Selain itu, kalibrasi yang berbeda antara dua arah dalam denah dapat sangat relevan untuk sistem asimetris (misalnya, ketika keberadaan tangga atau dinding pengisi diperhitungkan).
- Superposisi respons divalidasi melalui perbandingan dengan kurva kapasitas 3D yang diperoleh dari analisis nonlinier berbasis serat 3D. Pentingnya validasi ini adalah kemungkinan untuk mempelajari respons rangka 3D, yang memiliki rangka dengan geometri dan karakteristik resistensi yang berbeda, di bawah skenario pelepasan kolom pendukung tanpa perlu melakukan analisis 3D yang membutuhkan komputasi yang berat.
- Peningkatan ketahanan yang diadopsi telah menunjukkan efek yang menguntungkan dalam meningkatkan daya dukung sistem dan/atau mengantisipasi perilaku katenari dalam setiap skenario kegagalan. Hal ini penting, terutama untuk rangka yang memiliki balok dalam, di mana tulangan sisi muka sangat penting untuk mendukung mekanisme katenari. Peningkatan ini juga telah terbukti efektif dalam meningkatkan keuletan sistem.
- Pendekatan kesetaraan energi telah diterapkan pada kurva kapasitas global untuk menghitung titik kinerja untuk masing-masing dari tiga konfigurasi desain dan empat skenario kegagalan. Hasilnya telah menyoroti bagaimana, juga untuk skenario kegagalan yang paling menuntut, penyertaan kriteria ketahanan (misalnya, tulangan sisi muka) dalam desain rangka MR bidang memungkinkan tercapainya titik kinerja untuk perpindahan vertikal rendah, yang meningkatkan ketahanan struktural. Ini tidak berlaku untuk bangunan yang dirancang menurut aturan kode aktual, di mana titik kinerja tidak tercapai.
Oleh karena itu, desain struktur RC 3D dapat dilakukan melalui desain rangka MR yang memperhitungkan beberapa efek 3D yang relevan melalui pegas translasi non-linier dan menumpangkan efek respons NLFE planar pada dua arah ortogonal serta mematuhi prinsip seismik dan ketahanan. Peningkatan ketahanan konfigurasi tulangan C + (yaitu, dengan kriteria kontinuitas dan tulangan sisi muka) menunjukkan keseimbangan optimal antara peningkatan ketahanan struktural dan peningkatan keberlanjutan dalam terjadinya peristiwa ekstrem.
Akhirnya, perlu digarisbawahi bahwa kajian ini tidak memperhitungkan tangga apa pun dan efek membran pada pelat diabaikan karena kurang relevan dalam kasus pelat balok satu arah, sebagaimana tipologi bangunan yang diteliti dalam kajian ini.
