ABSTRAK
Model penetapan harga aset modal (CAPM) siap digunakan untuk menangkap hubungan linier antara pengembalian harian suatu aset dan indeks pasar. Kami memperluas model ini ke pengaturan frekuensi tinggi intraday dengan mengusulkan pendekatan estimasi CAPM fungsional. CAPM fungsional adalah contoh bergaya regresi linier fungsi-pada-fungsi dengan koefisien regresi fungsional bivariat. Koefisien regresi dua dimensi mengukur kovariansi silang antara pengembalian aset intraday kumulatif dan pengembalian pasar. Kami menerapkannya pada indeks Standard and Poor’s 500 dan saham-saham penyusunnya untuk menunjukkan kepraktisannya. Kami menyelidiki kecocokan dalam sampel dan prediksi di luar sampel CAPM fungsional untuk pengembalian intraday kumulatif suatu aset. Temuan-temuan menunjukkan bahwa metode CAPM fungsional yang diusulkan memiliki kecocokan model dan akurasi prakiraan yang lebih unggul dibandingkan dengan estimasi empiris CAPM tradisional. Secara khusus, metode fungsional menghasilkan kecocokan model dan akurasi prediksi yang lebih baik untuk saham-saham yang secara tradisional dianggap kurang efisien dalam hal harga atau lebih buram informasi.
1 Pendahuluan
Model penetapan harga aset modal (CAPM) (Sharpe 1964 ; Linter 1965 ) telah menjadi landasan keuangan teoritis dan empiris. Ini adalah model patokan dalam penelitian penetapan harga aset karena kesederhanaan dan efisiensinya dalam mengukur biaya ekuitas. CAPM berasumsi bahwa pasar sekuritas sangat kompetitif dan efisien, sehingga informasi yang relevan tentang perusahaan didistribusikan dan diserap dengan cepat dan universal. Ia juga berasumsi bahwa pasar-pasar ini didominasi oleh investor rasional dan penghindar risiko yang berusaha untuk memaksimalkan pengembalian atas investasi mereka; yaitu, mereka menuntut pengembalian yang lebih tinggi untuk risiko yang lebih besar. Oleh karena itu, harga aset memperhitungkan semua informasi yang tersedia di pasar yang efisien tanpa peluang arbitrase, dan pengembalian yang diharapkan dari suatu saham dipengaruhi oleh korelasinya dengan indeks pasar, yang diukur dengan beta.
Sejak diperkenalkannya CAPM, banyak perhatian telah diberikan pada peningkatan spesifikasi modelnya (lihat, misalnya, Casabona dan Vora 1982 ; Jagannathan dan Meier 2002 ; Bernardo et al. 2007 ). Misalnya, bukti yang cukup menunjukkan bahwa elemen-elemen dalam model CAPM, yaitu premi risiko pasar, suku bunga bebas risiko, dan beta, bervariasi dari waktu ke waktu (lihat, misalnya, Bollerslev et al. 1988 ; Fama dan French 1989 ; D’Souza et al. 1989 ; Jagannathan dan Wang 1996 ; Ghysels 1998 ; KQ Wang 2003 ; Ang dan Chen 2003 ; Zhou dan Paseka 2017 ), dan pemodelan kondisional yang secara eksplisit memungkinkan variasi temporal dalam pemuatan faktor menghasilkan perbaikan yang signifikan secara statistik dan bermakna secara ekonomi (lihat, misalnya, Ball dan Kothari 1989 ; Bera et al. 1988 ; Wiggins 1992 ; Braun et al. 1995 ; Ellis 1996 ; Fletcher 2002 ; Andersen et al. 2003 ; Bali et al. 2009 ; Bali et al. 2017 ; Zhou and Paseka 2017 ). Bali et al. ( 2017 ) berpendapat bahwa beta kondisional heteroskedastisitas autoregresif umum yang bervariasi berdasarkan waktu membantu menjelaskan variasi lintas sektoral dalam pengembalian saham yang diharapkan.
Berdasarkan CAPM bersyarat, Bollerslev et al. ( 2016 ) menggunakan estimasi berbasis frekuensi tinggi dan mengusulkan kerangka kerja penetapan harga aset yang menggunakan beta berkelanjutan untuk mencerminkan pergerakan intraday yang lancar di pasar dan dua beta kasar yang terkait dengan diskontinuitas harga intraday, atau lonjakan, selama bagian aktif dari hari perdagangan dan pengembalian penutupan-ke-pembukaan semalam, masing-masing. Lebih jauh, Bollerslev et al. ( 2022 ) mengusulkan “beta granular” yang memberikan tampilan yang jauh lebih baik pada ketergantungan inheren antara aset dan serangkaian faktor tertentu.
Literatur tentang beta yang bervariasi menurut waktu menyajikan banyak model yang mempertimbangkan waktu saat harga penutupan diamati. Namun, model-model ini sebagian besar mengabaikan perubahan dalam kurva harga intraday, yaitu, bagaimana instrumen keuangan bergeser dari waktu ke waktu. Data keuangan frekuensi tinggi, yaitu, pengamatan pada instrumen keuangan yang diambil dalam skala granular, seperti data transaksi per transaksi yang diberi cap waktu atau data tick-by-tick, dapat mengatasi kekurangan ini dengan lebih baik (lihat, misalnya, Brogaard et al. 2014 ; Brogaard et al. 2018 ; Chakrabarty et al. 2022 ). Dengan munculnya bursa baru, setiap transaksi daring dicatat dan dikompilasi ke dalam basis data, seperti jaringan komunikasi elektronik Pulau atau data untuk tawaran individual untuk membeli dan menjual.
Kemajuan terkini dalam penyimpanan komputer dan pengumpulan data telah memungkinkan peneliti di bidang keuangan untuk merekam dan menganalisis data frekuensi tinggi untuk memahami struktur mikro pasar yang terkait dengan penemuan harga dan efisiensi pasar (lihat, misalnya, Campbell et al. 1997 ; Engle 2000 ; Andersen 2000 ; Andersen et al. 2001 , 2003 ; Goodhart dan O’Hara 1997 ; Ghysels 2000 ; Wood 2000 ; Gençay et al. 2001 ; Gouriéroux dan Jasiak 2001 ; Lyons 2001 ; Andreou dan Ghysels 2002 ; Gençay et al. 2001 ; Tsay 2010 ; Papavassiliou 2013 ; Goldstein et al. 2014 ; Bollerslev et al. 2022 ). Aliran penelitian ini menunjukkan bahwa pengambilan sampel berbasis frekuensi tinggi memungkinkan representasi faktor yang lebih akurat dan prediksi harga aset yang lebih baik dibandingkan dengan estimasi frekuensi rendah konvensional, sehingga menghasilkan portofolio mean-variance ex post yang lebih efisien (Bollerslev dan Zhang 2003 ; Cenesizoglu et al. 2016 ; Hollstein et al. 2020a ). Andersen et al. ( 2004 , 13) memberikan bukti lebih lanjut yang menunjukkan bahwa pengukuran beta frekuensi tinggi mampu “menyoroti evolusi dinamis beta keamanan individual dengan lebih jelas” dibandingkan dengan hasil yang diperoleh dari data harian frekuensi rendah. Aue et al. ( 2012 ) memperkenalkan CAPM fungsional yang dimodifikasi dan prosedur pemantauan sekuensial dan menyarankan bahwa pendekatan analisis data fungsional berkinerja lebih baik dalam mendeteksi pemutusan struktural dan menangkap variabilitas waktu dalam beta.
Data keuangan intraday frekuensi tinggi adalah contoh data fungsional padat dalam statistik, yang direpresentasikan dalam bentuk grafik sebagai kurva (lihat, misalnya, Andersen et al. 2024 ). Sebagai bagian integral dari analisis data fungsional (Ramsay dan Silverman 2005 ; Ferraty dan Vieu 2006 ) dan analisis deret waktu (Kokoszka dan Reimherr 2017 ; Peña dan Rsay 2021 ), deret waktu fungsional terdiri dari fungsi acak yang diamati pada suatu interval waktu. Deret waktu fungsional dapat dikelompokkan ke dalam dua kategori, terlepas dari apakah kontinum tersebut juga merupakan variabel waktu. Di satu sisi, deret waktu fungsional dapat muncul dari pengukuran yang diperoleh dengan memisahkan catatan waktu yang hampir kontinu menjadi interval yang berurutan, misalnya, hari, minggu, atau tahun (lihat, misalnya, Hörmann dan Kokoszka 2012 ). Kami merujuk pada struktur data tersebut sebagai deret waktu fungsional yang diiris , contohnya termasuk kurva harga atau volatilitas intraday dari saham keuangan (lihat, misalnya, Shang 2017 ; Shang et al. 2019 ; Andersen et al. 2021 ). Di sisi lain, variabel fungsional dapat berupa variabel kontinu lainnya, seperti kurva hasil spesifik jatuh tempo (lihat, misalnya, Hays et al. 2012 ) atau panjang gelombang spektroskopi inframerah dekat (lihat, misalnya, Shang et al. 2022 ). Dalam kedua kasus tersebut, objek yang diminati adalah deret waktu diskrit dari fungsi dengan kontinum (lihat, misalnya, S. Wang et al. 2008 ; Kokoszka dan Zhang 2012 ; Kokoszka et al. 2017 ). Pada Bagian 2 , kami menjelaskan kumpulan data motivasi kami—pengembalian intraday kumulatif (CIDR) 5 menit dari indeks Standard and Poor’s 500 (S&P 500) dan komponennya. Kumpulan data ini termasuk dalam jenis pertama dari rangkaian waktu fungsional.
Jika harga dimodelkan sebagai deret waktu univariat dari observasi diskret, proses mendasar yang menghasilkan observasi ini tidak dapat ditemukan sepenuhnya. Keuntungan deret waktu fungsional mencakup yang berikut: (1) Berkat kontinuitas, kita dapat mempelajari korelasi temporal antara dua objek fungsional intraday. (2) Estimasi fungsi beta adalah gambar dua dimensi yang menangkap korelasi (silang) antara aset dan indeks sahamnya untuk mempelajari ketergantungan lintas-sektoral antara dua titik acak pada objek fungsional. (3) Kami menangani nilai yang hilang melalui teknik interpolasi atau penghalusan. (4) Dengan mengubah deret waktu univariat menjadi deret waktu fungsi, kami secara implisit mengatasi “kutukan dimensionalitas” (Donoho 2000 ), di mana teknik nonparametrik dan semiparametrik dapat diimplementasikan (lihat, misalnya, Ferraty dan Vieu 2006 ; Aneiros-Pérez dan Vieu 2006 ).
Kami mengusulkan perluasan CAPM yang disesuaikan untuk data keuangan frekuensi tinggi, yang disebut CAPM fungsional. CAPM fungsional baru-baru ini dipertimbangkan dalam makalah kerja Pedersen ( 2022 ). Namun, kami menyajikan cara baru untuk memperkirakan koefisien regresi dan menyelidiki perbedaan antara CAPM dan versi fungsionalnya dari aspek karakteristik perusahaan. Ini dirancang untuk menjelaskan seberapa banyak variabilitas (yaitu, informasi) dalam CIDR pasar dapat menjelaskan variabilitas dalam suatu aset. CAPM fungsional kami dapat dibentuk sebagai regresi linier fungsi-pada-fungsi, di mana tujuan kami adalah untuk memperkirakan koefisien regresi fungsional bivariat. Koefisien regresi fungsional bivariat mengukur hubungan linier antara respons fungsional (yaitu, CIDR suatu aset) dan prediktor fungsional (yaitu, CIDR suatu indeks pasar). Melalui CAPM fungsional, kami dapat memprediksi ekspektasi kondisional dalam sampel dari CIDR suatu aset dengan fungsi koefisien regresi bivariat yang diestimasi dan mengevaluasi kebaikan kesesuaian model melalui fungsionalTemuan dalam studi ini menunjukkan bahwa metode CAPM fungsional yang diusulkan menghadirkan kinerja yang lebih unggul dalam kesesuaian model untuk saham-saham yang kurang efisien dalam hal harga dan akurasi prediksi yang lebih baik untuk saham-saham yang tidak memiliki informasi yang cukup.
Artikel kami disusun sebagai berikut. Bagian 2 menjelaskan indeks pasar saham keuangan dan masing-masing saham penyusunnya. Bagian 3 memperkenalkan CAPM fungsional untuk memperkirakan fungsi koefisien regresi bivariat, yang menangkap hubungan linier antara indeks S&P 500 (SPX) dan saham penyusunnya. Kami menerapkan CAPM fungsional untuk memodelkan CIDR dengan memilih aset yang mewakili berbagai kelas aset. Di Bagian 4 , kami menampilkan fungsi koefisien regresi yang diperkirakan yang diperoleh dari regresi komponen utama fungsional (FPCR), regresi kuadrat parsial fungsional (FPLSR), dan regresi fungsi-pada-fungsi yang dikenai penalti (PFLM). , root mean squared error (RMSE) dan root mean squared prediction error (RMSPE) disajikan untuk meringkas kebaikan kecocokan dan prediksi di luar sampel untuk data keuangan intraday. Nilai terintegrasi dari kesalahan ini dapat digunakan untuk mengevaluasi dan membandingkan kebaikan kecocokan keseluruhan di antara berbagai saham konstituen di Bagian 5.1 dan 5.2 . Di Bagian 5.3 dan 5.4 , kami mengaitkan perbedaan dalam akurasi perkiraan antara CAPM klasik dan CAPM fungsional dengan karakteristik perusahaan dan tata kelola perusahaan, masing-masing. Bagian 6 menyimpulkan dan menawarkan beberapa ide tentang bagaimana metodologi yang disajikan dapat diperluas lebih lanjut. Rincian teknik FPCR, FPLSR, dan PFLM disajikan dalam Lampiran B – D.
2 Analisis Data Empiris
2.1 Pemilihan Data dan Sampel
S&P 500 adalah indeks pasar saham keuangan yang melacak kinerja sekitar 500 perusahaan besar yang terdaftar di bursa saham di Amerika Serikat. Riwayat tick intraday untuk SPX dan saham-saham penyusunnya diperoleh dari Refinitiv Datascope ( https://select.datascope.refinitiv.com/DataScope/ ). Kami mempertimbangkan pengembalian lintas-bagian harian dari 4 Januari 2021 hingga 31 Desember 2021. Pada tahun 2021, ada 252 hari perdagangan. Mengikuti karya awal oleh Bollerslev dan Zhang ( 2003 ), kami mengunduh harga transaksi untuk SPX dan setiap saham penyusun pada setiap interval 5 menit dari pukul 09:30 hingga 16:00. Untuk setiap saham, proses pengambilan sampel menghasilkan 78 titik data per hari dan sekitar 20.000 titik data dalam periode pengambilan sampel untuk analisis. Studi ini menggunakan 10 juta titik data intraday untuk demonstrasi. Ukuran sampel dapat diperluas tanpa kendala daya komputasi.
Kami memperoleh data tentang neraca keuangan dan sektor Global Industry Classification Standard (GICS) perusahaan dari Compustat. Data harian tentang pengembalian, harga, kapitalisasi pasar, dan volume diperoleh dari Center for Research in Security Prices (CRSP). Kepemilikan institusional diunduh dari arsip 13F. Data akurasi perkiraan pendapatan dan pengikut analis diunduh darifile ringkasan, dan informasi struktur papan diperoleh dari basis data BoardEx ( https://wrds-www.wharton.upenn.edu/pages/about/data-vendors/boardex/ ). Winsorisasi tidak dilakukan karena penanganan pengamatan ekstrem merupakan bagian dari pemodelan fungsional.
| Variabel | menit | Kuartil pertama | Rata-rata | Berarti | Kuartil ketiga | Maksimal |
|---|---|---|---|---|---|---|
| Harga intraday SPX | 3667 | 4074 | 4298 | 4274 | 4488 | 4808 |
| lnMCi,t | 7.889 | 9.843 | 10.434 | 10.555 | 11.139 | 14.659 |
| lnPi,t | 1.778 | 4.164 | 4.781 | 4.799 | 5.436 | 8.112 |
| LEVi,t | 0.102 | 0,505 | 0.653 | 0.640 | 0,774 tahun | 0,990 |
| VOLi,t(juta) | 2.191 | 20.075 | 40.540 | 91.834 | 89.521 | 1900.558 |
| ILLIQi,t(10 −9 ) | 0,001 | 0,031 | 0,063 tahun | 0,084 tahun | 0,108 | 1.872 |
| BidAskSpreadi,t | -8.452 | -7.991 | -7.806 | -7.758 | -7.622 | -4.361 |
| Coveragei,t | 0.2624 | 2.5871 | 2.8502 | 2.8059 | 3.1061 | 3.9269 |
| Accuracyi,t | 0.0000 | 0,0314 tahun | 0,0957 pukul 0,0957 | 0.3114 | 0.2962 | 6.0809 |
| InstoHoldi,t | 0,002 | 0.728 | 0.829 | 0.846 | 0.907 | 3.763 |
| Independenti,t | 0,5556 | 0.8333 | 0.9000 | 0.8723 | 0.9167 | 1.0000 |
| Dualityi,t A | 0.0000 | 1.0000 | 1.0000 | 0.8187 | 1.0000 | 1.0000 |
Variabel Biner, ada 411 angka satu dan 91 angka nol.
2.2 CIDR dari S&P 500
Kami mempertimbangkan data resolusi 5 menit, 78 titik data, yang mencakup periode dari pukul 9:30 hingga 16:00 Waktu Standar Timur. Untuk setiap aset, data harga penutupan intraday 5 menit,
, tersedia pada setiap hari perdagangan, yang kami gunakan untuk membangun urutan CIDR (lihat juga G. Rice et al. 2020 )
![]()
Di mana
menunjukkan aset di SPX,
menunjukkan
periode intraday ke-3,
menunjukkan hari perdagangan tertentu, dan
menunjukkan logaritma natural. Dari ( 1 ), kita mengambil transformasi invers untuk mendapatkan harga intraday 5 menit
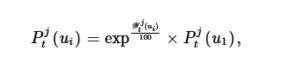
Di mana
menunjukkan harga penutupan awal pada hari tersebut
.
Pada suatu hari tertentu
, kami mengamati CIDR dari SPX dan saham-saham penyusunnya selama periode intraday.
menjadi prediktor fungsional, yang terdiri dari CIDR dari indeks pasar. Biarkan
menjadi respon fungsional, yang terdiri dari CIDR dari saham penyusun indeks. Biarkan
Dan
=
menjadi dua deret waktu fungsional respons dan prediktor, masing-masing. Biarkan
Dan
menunjukkan kelebihan pengembalian intraday suatu aset dan saham, dimana
.
dapat dihitung dengan membagi tingkat imbal hasil par treasury harian pada jatuh tempo 1 tahun dengan
waktu perdagangan intraday selama 251 hari perdagangan.
3 CAPM Fungsional
Sebelum menyajikan CAPM fungsional yang diusulkan, kami memberikan pemahaman intuitif tentang bagaimana kurva diperoleh dari data diskrit.
3.1 Dari Titik Data Diskrit ke Kurva
Dengan data keuangan frekuensi tinggi, titik-titik data diamati secara terpisah. Data keuangan intraday kami diamati secara padat pada grid yang berjarak sama, interval waktu 5 menit. Perluasan fungsi basis dapat mengubah titik-titik data terpisah menjadi fungsi kontinu. Karena itu, keuntungan dari pendekatan analisis data fungsional kami adalah pendekatan ini dapat mengatasi ketidaksinkronan, yaitu, interval waktu dengan panjang yang tidak teratur, dalam pengembalian aset saat diukur pada frekuensi tinggi (Dimson 1979 ; Lewellen dan Nagel 2006 ; Gilbert et al. 2014 ; Boguth et al. 2016 ).
Di antara semua fungsi basis yang mungkin, yang paling banyak digunakan adalah fungsi basis polinomial (yang dibangun dari monomial
), Fungsi dasar polinomial Bernstein (yang dibangun dari 1,
), Fungsi basis Fourier (yang dibangun dari 1,
), fungsi basis radial, fungsi basis wavelet, fungsi basis spline, dan fungsi basis ortogonal. Prediktor fungsional dan respons kami didekati dengan 20 fungsi basis B-spline:
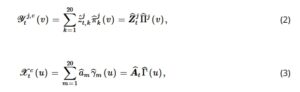
Di mana
Dan
adalah basis dan
Dan
adalah matriks koefisien yang bersesuaian.
Langkah pra-pemulusan ini memungkinkan kita untuk mengurangi kutukan dimensionalitas dengan memilih untuk bekerja dalam ruang fungsi yang dapat diintegrasikan secara kuadrat. Dari titik-titik data diskrit ini, kurva kontinu dapat dibangun dari
mewakili enam setengah jam perdagangan di Bursa Efek New York pada hari perdagangan.
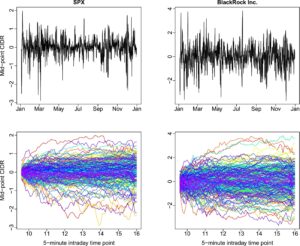
Deret waktu univariat dengan 19.327 pengembalian diskrit diubah menjadi
hari kurva CIDR. Pada Gambar 1 , kami menyajikan CIDR untuk S&P 500 dan BlackRock Inc. Menggunakan uji KPSS fungsional Horváth et al. ( 2014 ), kedua seri CIDR stasioner dengan
nilai masing-masing 0,669 dan 0,546.
3.2 CAPM Fungsional
CAPM klasik dapat diungkapkan sebagai
![]()
Di mana
Dan
menunjukkan aset harian dan pengembalian pasar,
menunjukkan tingkat bunga bebas risiko,
adalah parameter kemiringan bernilai riil yang terkait dengan aset, dan
menunjukkan istilah kesalahan dengan rata-rata nol dan varians terbatas.
CAPM fungsional menangkap hubungan linier antara prediktor fungsional yang terpusat dan respons fungsional yang terpusat melalui fungsi koefisien regresi bivariat yang tidak diketahui, yang dikenal sebagai permukaan beta. CAPM fungsional dapat dinyatakan sebagai
![]()
Di mana
menunjukkan tingkat bunga bebas risiko intraday,
menunjukkan premi risiko pasar intraday,
adalah fungsi koefisien regresi bivariat yang terkait dengan
saham konstituen,
menunjukkan fungsi kesalahan acak yang independen dan terdistribusi identik (iid), dan
menunjukkan rentang dukungan fungsi
(yaitu, periode perdagangan intraday antara pukul 9.30 dan 16.00 Waktu Standar Timur).
Pada ( 4 ), kami memodelkan hubungan antara respon fungsional
dan prediktor fungsional
melalui koefisien regresi bivariat
Untuk mencegah ketergantungan pada informasi masa depan (bias melihat ke depan), kami menyesuaikan batas integrasi sehingga untuk jangka waktu tertentu,
dalam interval
, integral pada ruas kanan persamaan ( 4 ) hanya mencakup nilai
untuk
Ini memastikan bahwa ketika memprediksi
, hanya informasi dari
sampai saat ini
digunakan, sehingga menjaga sifat kausal model.
CAPM fungsional adalah kasus khusus dari regresi linier fungsi-pada-fungsi yang terjadi bersamaan (lihat, misalnya, Ramsay dan Dalzell 1991 ). Estimasi langsung koefisien regresi dalam CAPM fungsional adalah masalah yang tidak tepat karena singularitas dan kutukan dimensionalitas. Karena prediktor dan respons fungsional termasuk dalam ruang fungsi berdimensi tak terhingga, kami mempertimbangkan untuk memproyeksikan prediktor dan respons fungsional ke basis ortonormal dan B-spline.
3.3 Estimasi Fungsi Koefisien Regresi
Dalam kerangka CAPM fungsional dalam ( 4 ), sangat penting untuk memperkirakan fungsi koefisien regresi bivariat secara akurat
dari sampel terbatas. Untuk tujuan ini, kami mengeksplorasi tiga metodologi berbeda: FPCR, FPLSR, dan PFLM. PFLM bergantung pada teknik perluasan basis umum seperti fungsi basis B-spline. FPCR dan FPLSR mengadopsi paradigma reduksi dimensi berbasis data, dan keduanya memerlukan proyeksi kurva berdimensi tak terhingga ke ruang berdimensi terbatas dari basis ortonormal. Sebaliknya, PFLM mungkin memerlukan sejumlah besar fungsi basis untuk memperkirakan koefisien regresi fungsional, yang berpotensi menyebabkan overfitting model dan mengurangi akurasi prediksi.
Dalam FPCR, komponen yang digunakan untuk memperkirakan fungsi koefisien regresi bivariatberasal dari kovariansi di antara prediktor fungsional saja. Beberapa komponen utama utama mencakup sebagian besar varians antara prediktor fungsional. Komponen laten ini mungkin tidak selalu penting untuk akurasi prediksi (lihat, misalnya, Delaigle dan Hall 2012 ). FPLSR mengatasi masalah ini dengan memanfaatkan respons dan prediktor saat mengekstraksi komponen laten, sehingga menangkap lebih banyak informasi dengan istilah yang lebih sedikit. Selain itu, penelitian telah menunjukkan bahwa FPLSR menawarkan estimasi fungsi parameter yang lebih akurat dibandingkan dengan FPCR, meskipun dengan pengurangan dimensi yang lebih besar (lihat, misalnya, Aguilera et al. 2010 ; Beyaztas dan Shang 2022 ; Saricam et al. 2022 ).
Baik dalam FPCR maupun FPLSR, basis ortogonal yang digerakkan oleh data mungkin tidak memiliki kehalusan pada parameter fungsional. Namun, hal ini dapat menyebabkan undersmoothing yang signifikan jika parameter fungsional menunjukkan kehalusan yang jauh lebih tinggi daripada skor FPLSR dan FPCR orde yang lebih tinggi (lihat, misalnya, Ivanescu et al. 2015 ; Beyaztas et al. 2025 ). Akibatnya, memasukkan satu atau dua komponen laten tambahan dapat mengubah bentuk dan interpretasi parameter fungsional (lihat juga Crainiceanu et al. 2009 ). Sebaliknya, dalam PFLM, istilah penalti yang diterapkan selama fase estimasi memaksakan tingkat kehalusan tertentu pada estimasi parameter, sehingga mencegah overfitting.
Rincian komprehensif mengenai metodologi FPCR, FPLSR, dan PFLM untuk memperkirakan fungsi koefisien regresi bivariat
dalam ( 4 ) telah ditangguhkan ke Lampiran B – D.
4 Ilustrasi CAPM Fungsional
Kami menerapkan FPCR dan FPLSR untuk memperkirakan fungsi koefisien regresi bivariat dalam CAPM fungsional. Kami mempertimbangkan CIDR dari SPX sebagai prediktor fungsional dan saham BlackRock Inc. sebagai respons fungsional untuk demonstrasi. Pada Gambar 2 , kami menampilkan fungsi koefisien regresi yang diperkirakan yang diperoleh dari dua model regresi fungsi-pada-fungsi. Fungsi koefisien regresi, yang diperkirakan oleh FPCR, menunjukkan aktivitas intens antara pukul 10:00 dan 11:30 dan antara pukul 13:30 dan 14:30. Sebaliknya, fungsi koefisien regresi yang diperkirakan oleh FPLSR menunjukkan aktivitas intens antara pukul 10:00 dan 11:30 dan antara pukul 15:00 dan 16:00.

Perbedaan antara permukaan beta yang diestimasi adalah karena karakteristik fungsi basis. Dalam FPCR, fungsi basis yang diperoleh dari prediktor fungsional bersifat ortonormal, dan tidak ada elemen off-diagonal. Dengan demikian, permukaan beta yang diestimasi relatif mulus. Sebaliknya, fungsi basis FPLSR yang diperoleh dari prediktor fungsional dan respons tidak ortogonal. Akar kuadrat terbalik dari matriks produk dalam memainkan peran penting dalam menghitung permukaan koefisien regresi FPLSR. Dalam fungsi basis FPLSR, elemen off-diagonal dari matriks produk dalam menangkap ketergantungan linier antara prediktor fungsional dan respons pada periode intraday yang berbeda. Akibatnya, FPLSR dapat menunjukkan lebih banyak fitur lokal daripada FPCR.
5 Estimasi Akurasi Respon
Dengan menggunakan CIDR milik BlackRock Inc., kami mengevaluasi dan membandingkan kinerja model dengan estimasi CAPM tradisional, FPCR, dan FPLSR. Pertama-tama kami mengukur kesesuaian dan akurasi estimasi FPCR dan FPLSR dalam sampel dengan menghitung
dan RMSE lalu menghitung RMSPE untuk mengukur akurasi prediksi di luar sampel selangkah lebih maju. Lebih lanjut, kami menyelidiki apakah karakteristik perusahaan, seperti sektor industri, ukuran perusahaan, leverage, likuiditas, dan ketidakpastian valuasi memengaruhi ukuran kinerja ini.
5.1 Kesesuaian Sampel
Meskipun fungsi koefisien regresi yang diestimasikan berbeda, kami menghitung versi intraday dari
dan RMSE sebagai dua kriteria kesesuaian dalam sampel.
dan kriteria RMSE diperluas dari model linier konvensional, yang didefinisikan sebagai
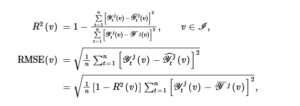
Di mana
mewakili nilai-nilai yang disesuaikan yang diperoleh dari CAPM fungsional, menggunakan fungsi koefisien regresi yang diestimasi.
Pada Gambar 3 , kami membandingkan intraday
dan RMSE antara CIDR yang diamati dan dipasang untuk BlackRock Inc. Di antara model-model tersebut, PFLM menunjukkan nilai tertinggi
nilai dan nilai RMSE terendah di seluruh interval intraday, yang menyoroti kecocokan dalam sampel yang kuat. Kinerja ini dicapai melalui mekanisme penalti yang memberlakukan batasan kelancaran pada permukaan koefisien regresi yang diestimasikan, yang secara efektif mengendalikan potensi overfitting.

Itu
Nilai untuk model PFLM mencapai level tertinggi antara pukul 10:30 pagi dan 12:00 siang, yang menunjukkan bahwa model tersebut menangkap sebagian besar variabilitas intraday selama periode aktivitas perdagangan yang meningkat ini. Setelah puncak ini,
tetap relatif stabil hingga sekitar pukul 2:00 siang, setelah itu secara bertahap menurun pada jam-jam perdagangan terakhir. Tren ini menunjukkan bahwa struktur penalti PFLM secara efektif menangkap dan mempertahankan hubungan prediktor-respons selama periode likuiditas dan volume perdagangan tinggi, sekaligus mencegah overfitting selama periode aktivitas rendah yang biasanya diamati pada sore hari.
Itu
Nilai untuk model PFLM mencapai level tertinggi antara pukul 10:30 pagi dan 12:00 siang, yang menunjukkan bahwa model tersebut menangkap sebagian besar variabilitas intraday selama periode aktivitas perdagangan yang meningkat ini. Setelah puncak ini,
tetap relatif stabil hingga sekitar pukul 2:00 siang, dan secara bertahap menurun pada jam-jam perdagangan terakhir. Tren ini menunjukkan bahwa struktur penalti PFLM secara efektif menangkap dan mempertahankan hubungan prediktor-respons selama likuiditas dan volume perdagangan tinggi sekaligus mencegah overfitting selama periode aktivitas rendah yang biasanya diamati pada sore hari.
Performa model PFLM yang unggul disebabkan oleh kontrol adaptifnya terhadap kompleksitas model. Penalti penghalusannya meminimalkan reaksi terhadap gangguan acak dalam data frekuensi tinggi, sehingga menghasilkan hasil yang stabil dan konsisten.
nilai sepanjang hari. Sebaliknya, FPCR dan FPLSR tidak memiliki fitur penalti ini, sehingga lebih sensitif terhadap fluktuasi, terutama selama jam perdagangan yang lebih sepi, ketika kebisingan pasar dapat memengaruhi prediksi model secara tidak proporsional.
Rata-rata
dan RMSE berguna jika seseorang membutuhkan ukuran kecocokan numerik tunggal. Mereka dapat dinyatakan sebagai
![]()
Semakin besar
nilai, semakin baik CAPM fungsional dapat menangkap hubungan linier keseluruhan antara prediktor dan respons. RMSE yang lebih kecil sering kali mencerminkan nilai yang lebih besar
nilai.
Kami menggunakan uji linearitas antara respons fungsional terdesentralisasi dan prediktor fungsional terdesentralisasi seperti yang diusulkan oleh Garcia-Portugués et al. ( 2021 ) untuk menguji hubungan linear antara pengembalian intraday suatu aset, yang dilambangkan sebagai
, dan stok
Hipotesis nol dirumuskan sebagai berikut:
![]()
Di mana
adalah operator Hilbert–Schmidt antara
ruang yang dapat direpresentasikan secara integral menggunakan kernel bivariat
, yaitu,
Tes ini mendefinisikan
melalui operator regresi integral yang diperoleh dengan memproyeksikan kovariat fungsional dan respons ke arah fungsional berdimensi terbatas. Statistik Cramér–von Mises, yang mengintegrasikan arah-arah ini, mengukur deviasi proses empiris dari rata-rata nol yang diharapkan. Statistik dikalibrasi menggunakan bootstrap liar yang efisien pada residual.
Hasil uji linearitas yang dilakukan pada tingkat signifikansi 0,05 menunjukkan adanya hubungan linear pada 449 perusahaan antara
Dan
Hal ini menunjukkan bahwa CAPM fungsional kami dapat menjelaskan secara memadai pengembalian intraday dari aset perusahaan-perusahaan ini. Sebaliknya, untuk 58 perusahaan yang tersisa, kami mengamati
nilai mendekati nol (yaitu,nilai < 0,05), yang menunjukkan adanya hubungan nonlinier antara laba intraday perusahaan-perusahaan ini dan saham. Ini berarti bahwa model yang lebih kompleks mungkin diperlukan untuk menangkap hubungan untuk subkelompok perusahaan ini secara akurat.
5.2 Akurasi Prediksi di Luar Sampel
Selain akurasi estimasi dalam sampel, kami membandingkan akurasi prediksi di luar sampel satu langkah lebih maju di antara metode dengan menghitung RMSPE. Total RMSPE didefinisikan sebagai berikut:

Kami mempertimbangkan pendekatan jendela yang meluas untuk membandingkan kinerja prediksi di luar sampel dari kedua metode. Untuk kedua kumpulan data, kami membagi
menjadi dua bagian: sampel pelatihan yang terdiri dari pertama
kurva dan sampel uji yang terdiri dari sisa
kurva. Kami memperoleh prakiraan satu langkah lebih maju untuk kurva ke-201 menggunakan seluruh pengamatan dalam set pelatihan. Kami menambah sampel pelatihan sebanyak 1 hari dan memperoleh prakiraan untuk kurva ke-202. Prosedur ini diulang hingga sampel pelatihan mencakup seluruh set data.
Input untuk estimasi CAPM tradisional adalah harga penutupan harian, dan beta adalah nilai riil. Sebaliknya, parameter dalam metode FPCR, FPLSR, dan PFLM diestimasi menggunakan data intraday, dan beta adalah permukaan dua dimensi. Secara intuitif, hasil dari keempat metode tersebut tidak dapat dibandingkan secara langsung karena sifat datanya. Oleh karena itu, kami telah melakukan integrasi untuk metode fungsional sehingga rata-rata dan median dari keempat ukuran kinerja untuk CAPM tradisional, FPCR, FPLSR, dan PFLM dapat dibandingkan.
Tabel 2 menampilkan estimasi dalam sampel menggunakan total
dan nilai RMSE antara holdout dan estimasi respon. Untuk saham-saham di SPX, kami merangkum hasil berdasarkan sektor GICS. Hasil yang disajikan pada Tabel 2 menunjukkan bahwa kesesuaian model (diukur dengan
) sangat bervariasi di antara berbagai industri. Namun, peringkat kebugaran model yang dihasilkan oleh keempat metode tersebut konsisten. CAPM tradisional menghasilkan nilai yang lebih tinggi
nilai-nilai yang lebih tinggi dibandingkan metode FPCR dan FPLSR namun memiliki kinerja yang lebih rendah dibandingkan metode PFLM. Teknologi Informasi, Keuangan, dan Industri merupakan sektor-sektor dengan nilai tertinggi.
nilai, sementara Utilitas dan Barang Pokok Konsumen memiliki kesesuaian terendah. Hal ini konsisten dengan literatur yang ada yang menemukan bahwa saham di beberapa industri memiliki harga yang lebih stabil dan mencerminkan informasi pribadi yang relatif lebih spesifik untuk perusahaan. Oleh karena itu, hal ini tercermin dalam kesesuaian yang lebih baik untuk perusahaan di industri tertentu ini (lihat, misalnya, Brogaard et al. 2022 ).
| TotalR2 | Total RMSE | |||||||
|---|---|---|---|---|---|---|---|---|
| Sektor | CAPM | FPCR | FPLSR | PFL | CAPM | FPCR | FPLSR | PFL |
| Energi (21) | 0.160 | 0,093 | 0.118 | 0.172 | 2.400 | 1.591 | 1.570 | 1.525 |
| Bahan (27) | 0.207 | 0,139 | 0.180 | 0.222 | 1.813 | 1.117 | 1.092 | 1.066 |
| Industri (69) | 0.234 | 0.154 | 0.205 | 0.246 | 1.897 | 0,993 tahun | 0,963 | 0,939 |
| Konsumen Diskresioner (59) | 0.202 | 0,136 | 0.180 | 0.220 | 2.028 | 1.292 | 1.258 | 1.228 |
| Barang Konsumsi Pokok (31) | 0,105 | 0,060 | 0.111 | 0,145 | 1.223 | 0.843 | 0.820 | 0.804 |
| Pelayanan Kesehatan (61) | 0,149 | 0.111 | 0,148 | 0.189 | 1.678 | 1.042 | 1.020 | 0,997 tahun |
| Keuangan (66) | 0.247 | 0.186 | 0.231 | 0.268 | 2.013 | 1.001 | 0,973 tahun | 0,952 |
| Teknologi Informasi (76) | 0.254 | 0.192 | 0.253 | 0.300 | 2.454 | 1.090 | 1.047 | 1.015 |
| Layanan Komunikasi (20) | 0.141 | 0,115 | 0.157 | 0.202 | 2.159 | 1.140 | 1.109 | 1.082 |
| Utilitas (28) | 0,079 tahun | 0,044 tahun | 0,087 tahun | 0.131 | 1.211 | 0.852 | 0.832 | 0.812 |
| Properti (30) | 0.160 | 0,070 | 0.121 | 0.151 | 1.630 | 0,987 | 0,960 | 0,944 tahun |
| Berarti | 0,176 tahun | 0.118 | 0.163 | 0.204 | 1.864 | 1.086 | 1.059 | 1.033 |
| Rata-rata | 0.160 | 0,115 | 0.157 | 0.202 | 1.897 | 1.042 | 1.020 | 0,997 tahun |
Ketika menyelidiki kecocokan dalam sampel (diukur dengan RMSE), metode PFLM kembali mengungguli metode yang sebanding dengan galat estimasi rata-rata dan median terkecil. Sektor dengan kecocokan dalam sampel yang lebih baik adalah Barang Pokok Konsumen dan Utilitas, sementara sektor Energi dan Barang Konsumsi Diskresioner memiliki galat prediksi dalam sampel yang relatif lebih besar. Secara keseluruhan, metode PFLM menyajikan keunggulan dengan akurasi estimasi dalam sampel.
Sebagai tampilan grafis, kami menyajikan plot biola pada Gambar 4 untuk membandingkan
dan nilai RMSE diperoleh dari CAPM dan CAPM fungsional dengan metode estimasi yang berbeda untuk berbagai sektor industri.

Tabel 3 menampilkan perbandingan model pada akurasi prakiraan di luar sampel menggunakan nilai RMSPE total. Hal ini menunjukkan bahwa FPCR adalah yang berkinerja terbaik dengan RMSPE terkecil, dan PFLM berada di peringkat kedua. CAPM tradisional adalah yang berkinerja terburuk, dengan kesalahan prakiraan tertinggi. Pengamatan ini konsisten terlepas dari sektor GICS saham. Hasil tersebut selanjutnya mengonfirmasi penerapan FPCR yang lebih luas untuk prakiraan di luar sampel (lihat, misalnya, H. Wang dan Cao 2023 , untuk perbandingan antara FPCR dan FPLSR).
| Jumlah total RMSPE | ||||
|---|---|---|---|---|
| Sektor | CAPM | FPCR | FPLSR | PFL |
| Energi (21) | 1.966 | 1.228 | 1.466 | 1.265 |
| Bahan (27) | 1.536 | 0.917 | 1.130 | 0,938 |
| Industri (69) | 2.102 | 0.867 | 1.230 | 0,878 |
| Konsumen Diskresioner (59) | 2.332 | 1.134 | 1.572 | 1.139 |
| Barang Konsumsi Pokok (31) | 1.287 | 0.732 | 1.186 | 0.753 |
| Pelayanan Kesehatan (61) | 1.855 | 0,918 tahun | 1.225 | 0.931 |
| Keuangan (66) | 2.768 | 0.832 | 1.097 | 0.837 |
| Teknologi Informasi (76) | 3.485 | 0,982 | 1.466 | 0,985 |
| Layanan Komunikasi (20) | 2.911 | 1.026 | 1.459 | 1.034 |
| Utilitas (28) | 1.135 | 0,669 tahun | 1.063 | 0,669 tahun |
| Properti (30) | 2.064 | 0.855 | 1.333 | 0,875 |
| Berarti | 2.131 | 0.924 | 1.293 | 0,937 tahun |
| Rata-rata | 2.064 | 0.917 | 1.230 | 0.931 |
Sebagai tampilan grafis, kami menyajikan plot biola pada Gambar 5 untuk membandingkan nilai RMSPE yang diperoleh dari CAPM dan CAPM fungsional dengan metode estimasi yang berbeda menurut berbagai sektor industri.
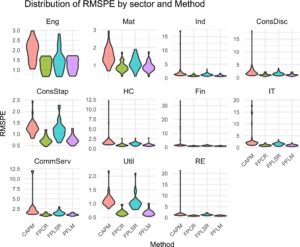
Metode PFLM berkinerja terbaik dalam kesesuaian model dan akurasi estimasi dalam sampel, sementara FPCR berkinerja terbaik dalam perkiraan di luar sampel. Metode fungsional yang disebutkan di atas menghadirkan kinerja yang lebih unggul daripada CAPM tradisional. Ini karena CAPM tradisional hanya menggunakan satu observasi untuk hari perdagangan (harga penutupan yang dicatat pada pukul 16:00); metode ini sangat teragregasi dan mengabaikan banyak informasi yang tertanam dalam fluktuasi intraday. Di sisi lain, metode fungsional memanfaatkan data intraday (78 titik data) untuk satu hari perdagangan. Metode fungsional memanfaatkan fungsi basis B-spline untuk merekonstruksi kurva halus dari data diskrit. Jumlah penghalusan yang memadai mengurangi kesalahan pengukuran data yang sering diabaikan oleh CAPM tradisional.
Untuk menilai ketahanan temuan kami dari data tahun 2021, kami melakukan analisis sensitivitas di Lampiran A dengan mereplikasi studi menggunakan data intraday frekuensi tinggi dari tahun 2020.
5.3 Karakteristik Perusahaan dan Kinerja Model
Kami membandingkan ukuran kinerja model di antara keempat metode dan menyelidiki apakah karakteristik perusahaan memengaruhi ukuran ini. Kami mengurutkan masing-masing perusahaan S&P 500 berdasarkan karakteristik perusahaan, kemudian mengadopsi dua sampel
pengujian untuk menyelidiki apakah kinerja model (diukur dengan
, RMSE, dan RMSPE) berbeda secara signifikan antara kelompok subsampel desil atas dan bawah. Kami mengikuti Brogaard et al. ( 2022 ) dan menyelidiki karakteristik perusahaan berikut: log kapitalisasi pasar (
), harga saham log (
), dan leverage (
Kami mengikuti Kumar ( 2009 ) dan mengadopsi volume turnover (
) terhadap ketidakpastian penilaian proksi, yang diukur sebagai rasio jumlah saham yang diperdagangkan dalam sebulan dan jumlah saham yang beredar. Selanjutnya, kami menyertakan dua ukuran ilikuiditas dan biaya perdagangan untuk menangkap batasan arbitrase. Yang pertama adalah ukuran ilikuiditas (
) dalam Amihud ( 2002 ) dan Bali et al. ( 2009 ), yang didefinisikan sebagai rasio rata-rata pengembalian absolut harian terhadap volume perdagangan (dolar) pada hari itu. Yang kedua adalah rata-rata spread bid–ask efektif saham (
), yang diukur dengan logaritma natural dari rata-rata spread efektif harian.
Tabel 4 menyajikan hasil perbedaan rata-rata kinerja model ketika membandingkan perusahaan dengan karakteristik yang berbeda. Untuk kesesuaian model, yang diukur dengan
, keempat metode menunjukkan kinerja yang jauh lebih unggul untuk (
) dan harga lebih tinggi (
) saham. Hal ini konsisten dengan penelitian sebelumnya dalam literatur yang menunjukkan bahwa perusahaan yang lebih besar lebih transparan dan likuid dan, oleh karena itu, memiliki harga yang lebih efisien (Brogaard et al. 2022 ). Ketiga metode fungsional menghasilkan kesesuaian model yang jauh lebih baik untuk saham dengan ilikuiditas yang lebih tinggi (
), dan FPCR dan PFLM berkinerja lebih baik untuk perusahaan dengan spread bid–ask yang lebih tinggi (
). Hal ini menunjukkan bahwa metode fungsional memberikan kesesuaian model yang lebih unggul untuk saham yang kurang likuid dengan biaya perdagangan yang lebih besar daripada CAPM tradisional.
| R2 | RMSE | RMSPE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Karakteristik perusahaan | CAPM | FPCR | FPLSR | PFL | CAPM | FPCR | FPLSR | PFL | CAPM | FPCR | FPLSR | PFL | |
| lnMCi,t | Tinggi | 0.227 | 0,167 | 0.212 | 0.260 | 1.494 | 0,869 | 0.845 | 0.819 | 1.554 | 0.800 | 1.051 | 0,798 tahun |
| Rendah | 0.152 | 0,108 | 0.152 | 0.191 | 2.324 | 1.324 | 1.289 | 1.261 | 2.881 | 1.118 | 1.644 | 1.137 | |
| tstatistik | 3.208 | 3.676 | 3.323 | 3.901 | -3.059 | -6.246 | -6.248 | -6.383 | -2.699 | -4.555 | -5.239 | -4.911 | |
| pnilai | 0,002 | 0,001 | 0,001 | 0.000 | 0,003 | 0.000 | 0.000 | 0.000 | 0,010 | 0.000 | 0.000 | 0.000 | |
| Tanda tangan. | *** | *** | *** | *** | ** | *** | *** | *** | *** | *** | *** | *** | |
| lnPi,t | Tinggi | 0,235 | 0.173 | 0.220 | 0.268 | 2.173 | 1.064 | 1.032 | 1.002 | 3.347 | 0.962 | 1.371 | 0,960 |
| Rendah | 0.160 | 0,108 | 0,148 | 0.188 | 2.094 | 1.344 | 1.314 | 1.284 | 2.145 | 1.087 | 1.530 | 1.110 | |
| tstatistik | 3.361 | 4.576 | 4.470 | 5.066 | 0.269 | -3.903 | -3.990 | -4.085 | 1.762 | -1.949 | -1.511 | -2,343 | |
| pnilai | 0,001 | 0.000 | 0.000 | 0.000 | 0,789 tahun | 0.000 | 0.000 | 0.000 | 0,083 tahun | 0,054 tahun | 0,134 tahun | 0,021 | |
| Tanda tangan. | *** | *** | *** | *** | *** | *** | *** | * | |||||
| LEVi,t | Tinggi | 0.192 | 0,135 | 0.182 | 0.220 | 2.091 | 1.081 | 1.052 | 1.028 | 2.939 | 0,958 | 1.339 | 0,970 |
| Rendah | 0.221 | 0.160 | 0.214 | 0,258 | 2.591 | 1.129 | 1.093 | 1.061 | 3.518 | 0,993 tahun | 1.411 | 0,996 tahun | |
| statistik | -0,331 | -1,093 | -0,722 | -0,943 | 0,665 tahun | 0.616 | 0,588 | 0.601 | 0.347 | -0,146 | 1.429 | 0,037 hari | |
| pnilai | 0.742 | 0,278 | 0.472 | 0,348 tahun | 0,508 tahun | 0,540 | 0,558 | 0,550 | 0.730 | 0.884 | 0.157 | 0,971 tahun | |
| Tanda tangan. | |||||||||||||
| VOLi,t | Tinggi | 0.164 | 0.110 | 0.159 | 0.201 | 1.726 | 1.048 | 1.017 | 0,992 | 1.998 | 0.890 | 1.302 | 0.901 |
| Rendah | 0.187 | 0,136 | 0.182 | 0.226 | 2.352 | 1.035 | 1.006 | 0,979 tahun | 3.288 | 0.907 | 1.294 | 0.920 | |
| tstatistik | -0,932 | -0,799 | -1,153 | -0,880 | -0,107 | 3.236 | 3.273 | 3.254 | -2.423 | 2.849 | 1.227 | 2.943 | |
| pnilai | 0.354 | 0.426 | 0.252 | 0.381 | 0,915 | 0,002 | 0,002 | 0,002 | 0,019 | 0,006 | 0.224 | 0,005 | |
| Tanda tangan. | *** | *** | *** | * | ** | ** | |||||||
| ILLIQi,t | Tinggi | 0,185 | 0.126 | 0.169 | 0.212 | 1.848 | 1.047 | 1.021 | 0,995 | 1.879 | 0,868 | 1.208 | 0.881 |
| Rendah | 0.152 | 0.113 | 0.161 | 0.202 | 2.286 | 1.140 | 1.107 | 1.081 | 3.222 | 0,999 | 1.417 | 1.010 | |
| tstatistik | -1.654 | -2.558 | -2,355 | -3.005 | 2.151 | 4.807 | 4.786 | 5.011 | 1.940 | 2.402 | 3.238 | 2.795 | |
| pnilai | 0.102 | 0,012 | 0,021 | 0,004 tahun | 0,035 | 0.000 | 0.000 | 0.000 | 0,058 | 0,018 | 0,002 | 0,006 | |
| Tanda tangan. | * | * | ** | ** | *** | *** | *** | * | ** | ** | |||
| BidAskSpreadi,t | Tinggi | 0.216 | 0,135 | 0.187 | 0.226 | 1.539 | 0,983 | 0,952 | 0.930 | 1.796 | 0.850 | 1.259 | 0.864 |
| Rendah | 0.193 | 0.133 | 0,177 tahun | 0.220 | 1.719 | 1.046 | 1.018 | 0,992 | 2.119 | 0,895 | 1.262 | 0.901 | |
| tstatistik | 0,938 | 2.400 | 1.679 | 2.040 | 4.499 | 6.562 | 6.483 | 6.471 | 3.170 | 6.317 | 5.782 | 6.140 | |
| pnilai | 0.351 | 0,018 | 0,096 tahun | 0,044 tahun | 0.000 | 0.000 | 0.000 | 0.000 | 0,003 | 0.000 | 0.000 | 0.000 | |
| Tanda tangan. | * | * | *** | *** | *** | *** | ** | *** | *** | *** | |||
Catatan: Definisi karakteristik perusahaan didefinisikan: adalah kapitalisasi pasar log untuk perusahaan pada waktu , Dan adalah harga log. adalah leverage yang diukur dengan rasio total liabilitas terhadap total aset. perputaran volume bulanan adalah proksi ketidakpastian penilaian, yang diukur sebagai rasio jumlah saham yang diperdagangkan dalam sebulan dan jumlah saham yang beredar. adalah ukuran illiquiditas Amihud ( 2002 ), yang diukur dengan rasio rata-rata pengembalian absolut harian terhadap volume perdagangan (dolar) pada hari itu. adalah rata-rata spread bid–ask efektif, yang diukur dengan logaritma natural dari rata-rata spread harian efektif. * Signifikansi pada 0,05. ** Signifikansi pada 0,01. *** Signifikansi pada 0,001.
Saat mengukur kecocokan dalam sampel, keempat metode menghasilkan RMSE yang jauh lebih kecil untuk saham dengan kapitalisasi pasar yang lebih besar (
), tingkat likuiditas yang lebih tinggi (
), dan biaya perdagangan yang lebih besar (
). Terlihat juga bahwa ketiga metode fungsional tersebut memberikan kinerja yang jauh lebih baik untuk saham dengan harga yang lebih tinggi (
) dan saham dengan perputaran volume bulanan yang lebih rendah (
). Pada saat yang sama, perbedaan kinerja untuk CAPM tradisional tidak diamati untuk saham tersebut. Hasil pengujian untuk akurasi perkiraan di luar sampel serupa. RMSPE secara signifikan lebih kecil untuk saham dengan kapitalisasi pasar yang lebih besar (
) dan biaya perdagangan yang lebih besar (
). Demikian pula, ketiga metode fungsional tersebut memberikan kinerja yang jauh lebih baik bagi perusahaan dengan tingkat ilikuiditas yang lebih tinggi (
), sementara perbedaan kinerja untuk CAPM tradisional tidak teramati.
5.4 Tata Kelola Perusahaan dan Kinerja Model
Kami juga menyelidiki kinerja model karena faktor pemantauan eksternal dan tata kelola perusahaan. Kami mengadopsi variabel pengikut analis dan kepemilikan institusional untuk mengukur efek pemantauan eksternal. Analis keuangan mengumpulkan informasi dari berbagai sumber, menilai kinerja perusahaan saat ini, memperkirakan prospek masa depan, dan memberikan rekomendasi beli, tahan, atau jual kepada investor. Literatur sebelumnya menunjukkan analis mengurangi asimetri informasi di berbagai dimensi, bertindak sebagai pemantau eksternal bagi manajer perusahaan. Akibatnya, mereka memengaruhi investasi perusahaan, keputusan pembiayaan, harga saham, likuiditas, dan valuasi (He dan Tian 2013 ; Hong et al. 2000 ; Derrien dan Kecskes 2013 ). Untuk menyelidiki efek pengikut analis pada kinerja model, kami mengadopsi cakupan analis yang banyak digunakan (
) (He dan Tian 2013 ) dan kesalahan perkiraan analis (
) (Payne 2008 ) mengukur.
diukur sebagai
![]()
Di mana
adalah rata-rata dari 12 angka perkiraan pendapatan bulanan untuk perusahaan
di tahun
dan angka perkiraan diperoleh dari
file ringkasan. File yang lebih besar
menunjukkan pengawasan eksternal yang lebih kuat.
Mengikuti Payne ( 2008 ), kami mengukur kesalahan perkiraan analis (
) sebagai
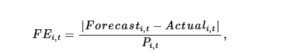
Di mana
adalah rata-rata ramalan yang dibuat oleh setiap analis untuk perusahaan
di tahun
sebelum tanggal pengumuman pendapatan klien dan
adalah pendapatan aktual perusahaan pada tahun tersebut
Nilai absolut dari kesalahan perkiraan dideflasi oleh harga saham terbaru yang tersedia. Kesalahan perkiraan yang lebih kecil dalam pengukuran (
) menunjukkan keakuratan perkiraan yang lebih besar.
Kepemilikan institusional (
) diukur sebagai persentase saham beredar yang dimiliki oleh investor institusional. Secara umum diakui bahwa investor institusional adalah pedagang yang terinformasi di pasar yang bertanggung jawab untuk menahan informasi harga dan berkontribusi pada efisiensi pasar melalui perdagangan mereka (Boehmer dan Kelley 2009 ). Perusahaan yang berada di bawah pengaruh pemantauan eksternal yang lebih besar diharapkan memberikan informasi khusus perusahaan dengan kualitas yang lebih tinggi untuk memungkinkan kesesuaian model yang lebih baik dan kesalahan perkiraan yang lebih kecil. Kami mengadopsi dua variabel struktur dewan tambahan untuk mengukur tata kelola perusahaan yang efektif. Mengikuti Linck et al. ( 2008 ), kami menggunakan independensi dewan yang diukur dengan proporsi direktur independen luar (
), dan kepemimpinan dewan dengan variabel dummy satu jika CEO adalah ketua dewan (
).
Tabel 5 menyajikan hasil perbedaan rata-rata untuk kinerja model ketika membandingkan perusahaan dengan tingkat pemantauan eksternal dan tata kelola perusahaan yang berbeda. Untuk kesesuaian model, ketiga metode tersebut berkinerja lebih baik secara signifikan untuk perusahaan dengan cakupan analis yang lebih tinggi (
) dan akurasi perkiraan analis yang lebih tinggi (yaitu, lebih rendah
). Hal ini konsisten dengan penelitian yang menemukan bahwa perusahaan dengan jumlah analis yang lebih banyak menghasilkan informasi spesifik perusahaan yang lebih transparan, yang meningkatkan efisiensi harga. Selain itu, ketiga metode fungsional tersebut memberikan hasil yang lebih baik.
untuk perusahaan dengan proporsi direktur independen yang lebih rendah, sementara tidak ada perbedaan yang diamati untuk metode CAPM tradisional. Untuk estimasi dalam sampel, keempat metode memberikan kesalahan estimasi yang jauh lebih kecil untuk saham dengan akurasi perkiraan analis yang lebih tinggi, dan tiga metode fungsional berkinerja lebih baik untuk perusahaan dengan kepemilikan institusional yang lebih tinggi (
). Untuk prediksi out-of-sample, ketika menggunakan metode fungsional, RMSPE secara signifikan lebih kecil untuk perusahaan dengan akurasi perkiraan analis yang lebih baik (lebih rendah
) dan kepemilikan institusional yang lebih tinggi (
). Konsisten dengan temuan sebelumnya, ketiga metode fungsional menghasilkan RMSE yang jauh lebih kecil daripada metode CAPM tradisional untuk estimasi dalam sampel dan prediksi di luar sampel.
| Analis mengikuti dan | R2 | RMSE | RMSPE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tata kelola perusahaan | CAPM | FPCR | FPLSR | PFL | CAPM | FPCR | FPLSR | PFL | CAPM | FPCR | FPLSR | PFL | |
| Coveragei,t | Tinggi | 0,259 | 0,176 tahun | 0,225 | 0.270 | 1.816 | 1.052 | 1.021 | 0,991 tahun | 1.806 | 0,964 tahun | 1.328 | 0,954 |
| Rendah | 0.170 | 0.106 | 0.151 | 0.188 | 1.938 | 1.064 | 1.037 | 1.015 | 2.638 | 0,928 | 1.362 | 0.943 | |
| tstatistik | 4.185 | 5.366 | 5.056 | 5.393 | -0,351 | -0,200 | -0,275 | -0,413 | -1,227 | 0.622 | -0,388 | 0.197 | |
| pnilai | 0.000 | 0.000 | 0.000 | 0.000 | 0.727 | 0.842 | 0.784 | 0.680 | 0,225 | 0,536 tahun | 0,699 tahun | 0.844 | |
| Tanda tangan. | *** | *** | *** | *** | |||||||||
| FEi,t | Tinggi | 0,185 | 0,125 | 0.171 | 0.211 | 2.195 | 1.160 | 1.131 | 1.104 | 2.059 | 0,976 tahun | 1.409 | 0,998 |
| Rendah | 0.210 | 0.142 | 0.190 | 0.233 | 2.100 | 1.105 | 1.074 | 1.047 | 2.859 | 0,966 tahun | 1.333 | 0,975 | |
| tstatistik | -2.690 | -3.665 | -3,154 | -3.604 | 2.298 | 5.695 | 5.649 | 5.716 | 2.068 | 4.484 | 4.284 | 4.712 | |
| pnilai | 0,009 | 0.000 | 0,002 | 0,001 | 0,024 | 0.000 | 0.000 | 0.000 | 0,041 tahun | 0.000 | 0.000 | 0.000 | |
| Tanda tangan. | ** | *** | ** | *** | * | *** | *** | *** | * | *** | *** | *** | |
| InstoHoldi,t | Tinggi | 0.188 | 0.132 | 0.187 | 0.223 | 1.995 | 1.065 | 1.030 | 1.009 | 2.694 | 0.908 | 1.339 | 0.920 |
| Rendah | 0,167 | 0.117 | 0.160 | 0.201 | 1.929 | 1.209 | 1.182 | 1.153 | 2.162 | 0,998 | 1.322 | 1.013 | |
| tstatistik | 0.502 | 1.885 | 0.681 | 0.844 | 4.316 | 6.615 | 6.471 | 6.453 | 2.260 | 5.939 | 2.450 | 5.573 | |
| pnilai | 0.660 | 0.162 | 0,559 | 0,475 tahun | 0.000 | 0.000 | 0.000 | 0.000 | 0,029 | 0.000 | 0,075 hari | 0.000 | |
| Tanda tangan. | *** | *** | *** | *** | * | *** | *** | ||||||
| Independenti,t | Tinggi | 0.196 | 0.116 | 0,158 | 0.202 | 1.816 | 1.074 | 1.049 | 1.023 | 1.816 | 0.890 | 1.245 | 0.910 |
| Rendah | 0.210 | 0,147 tahun | 0.192 | 0.229 | 1.839 | 1.186 | 1.157 | 1.131 | 2.055 | 0,990 | 1.391 | 1.004 | |
| tstatistik | -1,067 | -2.556 | -2.546 | -2.806 | -1.070 | -0,851 | -0,755 | -0,715 | -1,039 | -1.702 | -1,362 | -1,232 | |
| pnilai | 0.289 | 0,013 | 0,013 | 0,006 | 0.288 | 0,398 | 0.453 | 0.477 | 0.302 | 0,093 | 0,177 tahun | 0.222 | |
| Tanda tangan. | * | * | ** | ||||||||||
| Dualityi,t | Tinggi | 0.196 | 0,134 tahun | 0.181 | 0.222 | 1.946 | 1.080 | 1.050 | 1.024 | 2.306 | 0.924 | 1.315 | 0,935 |
| Rendah | 0.188 | 0.127 | 0.173 | 0.212 | 1.825 | 1.102 | 1.073 | 1.049 | 2.178 | 0.941 | 1.317 | 0,958 | |
| tstatistik | 0,558 | 0,769 tahun | 0.837 | 1.082 | 0.819 | -0,515 | -0,543 | -0,602 | 0.397 | -0,478 | -0,027 | -0,613 | |
| pnilai | 0,578 | 0.443 | 0.404 | 0.281 | 0.414 | 0.607 | 0,588 | 0,549 tahun | 0.692 | 0.634 | 0,978 tahun | 0,541 tahun | |
| Tanda tangan. | |||||||||||||
Catatan: Definisi karakteristik perusahaan: adalah logaritma natural dari satu ditambah rata-rata 12 angka perkiraan pendapatan bulanan. diukur berdasarkan kesalahan perkiraan pendapatan analis yang absolut dikurangi dengan harga saham terkini yang tersedia, yang mana kesalahan perkiraan sama dengan perkiraan konsensus analis dikurangi pendapatan aktual. adalah persentase saham beredar yang dimiliki investor institusional. adalah proporsi direktur independen luar. adalah variabel dummy yang sama dengan satu jika CEO merupakan ketua dewan. * Signifikansi pada 0,05. ** Signifikansi pada 0,01. *** Signifikansi pada 0,001.
Lebih jauh, kami menguji efisiensi komputasional setiap metode dengan mencatat waktu yang telah berlalu yang diperlukan untuk menyesuaikan kumpulan data saham individual. Karena setiap metode diterapkan secara independen pada setiap kumpulan data, kami melaporkan waktu komputasi rata-rata di semua saham. Temuan kami mengungkapkan bahwa, rata-rata, CAPM, FPCR, FPLSR, dan PFLM memerlukan 0,010, 3,729, 0,097, dan 7,924 detik, masing-masing, untuk menyesuaikan satu kumpulan data. Seperti yang diantisipasi, CAPM adalah metode yang paling efisien secara komputasi. FPLSR menunjukkan efisiensi komputasi yang lebih besar di antara model regresi fungsional, yang membutuhkan lebih sedikit waktu daripada FPCR dan PFLM. Khususnya, PFLM menunjukkan biaya komputasi tertinggi, sebagian besar karena penggunaan algoritma penalti dan prosedur pencarian grid untuk mengoptimalkan parameter regularisasi, yang secara signifikan meningkatkan waktu komputasi keseluruhan. Kami mencatat bahwa komputasi dilakukan menggunakan R 4.2.2 pada PC Intel Core i7 6700HQ 2,6-GHz.
Singkatnya, studi ini menemukan bahwa PFLM yang diusulkan di sini berkinerja lebih baik dalam model goodness of fit dan in-sample fitting daripada CAPM tradisional. Pada saat yang sama, metode FPCR menghasilkan prediksi out-of-sample terbaik di antara model yang sebanding. Hasilnya juga menunjukkan bahwa karakteristik perusahaan secara signifikan memengaruhi kinerja model fungsional. Metode fungsional mengungguli CAPM tradisional untuk saham dalam model goodness of fit dengan biaya perdagangan yang lebih besar dan illiquiditas. Temuan serupa terbukti dalam prediksi bahwa metode fungsional berkinerja lebih baik untuk perusahaan dengan turnover volume bulanan yang lebih rendah, illiquiditas yang lebih besar, dan bid–ask spread yang lebih besar. Perusahaan-perusahaan tersebut biasanya dianggap lebih buram informasi (Amihud 2002 ; Brogaard et al. 2022 ), jadi di situlah kita melihat penggunaan data frekuensi yang lebih tinggi dan metode fungsional jauh lebih unggul untuk penetapan harga aset, memperkuat kemampuan mereka untuk menangkap informasi spesifik perusahaan dan dinamika harga secara lebih efektif daripada CAPM tradisional.
6 Kesimpulan
Mengingat jumlah data keuangan frekuensi tinggi yang terus meningkat, kami mengusulkan perluasan CAPM di mana prediktor dan respons adalah variabel bernilai fungsi. Dengan data frekuensi tinggi, CAPM fungsional adalah pendekatan baru untuk menguji model klasik secara empiris dengan mempelajari hubungan linier antara saham dan indeks pasar. Pendekatan fungsional dapat memungkinkan risiko yang disumbangkan oleh saham individual terhadap portofolio keseluruhan untuk dikelola dengan lebih baik. Secara keseluruhan, estimasi CAPM fungsional memungkinkan peningkatan optimalisasi portofolio (lihat, misalnya, Hollstein et al. 2020a , 2020b ; Drobetz et al. 2024 ). Kami mempertimbangkan FPCR, FPLSR, dan PFLM untuk memperkirakan fungsi koefisien regresi bivariat dalam regresi linier fungsi-pada-fungsi bersamaan ini. Fungsi koefisien regresi yang diestimasikan mengukur hubungan linier antara prediktor fungsional dan respons. Kami dapat memperoleh respons yang disesuaikan dengan fungsi koefisien regresi yang diestimasikan dan membandingkan nilainya dengan yang ditahan. Melalui intraday dan total
dan RMSE, kami mengevaluasi dan membandingkan kesesuaian antara indeks pasar dan konstituennya menggunakan CAPM fungsional. Melalui RMSPE, kami juga mempelajari akurasi prakiraan di luar sampelnya, yang dapat dibagi menjadi berbagai sektor industri GICS. Temuan dalam studi ini menunjukkan bahwa PFLM, bersama dengan data frekuensi tinggi, menyajikan kesesuaian dalam sampel yang unggul, sementara metode FPCR berkinerja terbaik dalam hal prediksi di luar sampel, diikuti oleh PFLM. CAPM fungsional memberikan kesesuaian model dan akurasi prediksi yang lebih baik untuk saham yang kurang hemat harga atau lebih buram informasi daripada CAPM tradisional.
Setidaknya ada empat cara di mana metodologi yang disajikan dapat diperluas. (1) Kami menggunakan data intraday 1 tahun, tetapi analisisnya dapat dilakukan untuk periode yang lebih lama. (2) CAPM fungsional adalah contoh model linier fungsi-pada-fungsi bersamaan. Mengikuti Corsi ( 2009 ) dan Hollstein et al. ( 2020a ), salah satu perluasannya adalah dengan menambahkan variabel tertinggal dari variabel respons.
, Dan
mewakili CIDR harian, mingguan, dan bulanan masa lalu
saham. (3) Mengikuti Qi dan Luo ( 2019 ), perluasan lainnya adalah mempertimbangkan regresi fungsi-pada-fungsi nonlinier , di mana permukaan beta dapat diestimasi secara nonparametrik. Ini merupakan peluang untuk penyelidikan lebih lanjut. CAPM fungsional mengasumsikan hubungan linier antara prediktor fungsional dan respons. Kami memvalidasi asumsi ini dengan melakukan uji linearitas, yang menunjukkan bahwa struktur linier ini sesuai untuk lebih dari 400 saham dalam kumpulan data kami. Namun, mengingat potensi ketergantungan nonlinier dalam data keuangan, terutama pada frekuensi tinggi, penting untuk mengakui keterbatasan asumsi ini. Kerangka kerja fungsional kami dapat diadaptasi jika hubungan nonlinier hadir dengan memanfaatkan fungsi basis alternatif, seperti basis polinomial atau wavelet, untuk memperkirakan pola nonlinier. Fleksibilitas ini memungkinkan kami untuk memperluas model untuk mengakomodasi nonlinier sebagaimana diperlukan. (4) Kesalahan spesifikasi model karena nonlinier yang tidak dimodelkan dapat memengaruhi kinerja CAPM fungsional, yang berpotensi menyebabkan estimasi yang bias. Pekerjaan di masa mendatang dapat mengeksplorasi model regresi fungsi-pada-fungsi nonlinier untuk memperhitungkan dinamika ini, meningkatkan ketahanan model dalam berbagai kondisi pasar.
